Por tercera vez en los últimos cinco años (cuarta, si cuento otra universidad) me toca dar un curso de probabilidades y estadísticas. Así que es hora de buscarme nuevas historias para contar (el público siempre se renueva... al menos en la mayor parte, pero soy yo el que comienzo a aburrirme).
* * *Abraham Wald era austro-húngaro (estrictamente, rumano). Un dato menor, sobre alguien conocido por sus trabajos en estadística, pero otro de la larga lista de científicos de primer nivel que estaban activos durante la segunda guerra mundial trabajando para los yanquis.
Por ejemplo,
von Neumann,
von Karman,
Wigner,
Teller,
Szilard... todos ellos húngaros, podrían haber desarrollado la bomba en Europa, y hoy otra sería la historia del mundo.
Cuentan que cierto día, hablando en Los Alamos durante un almuerzo sobre la existencia o no de extraterrestres, todos coincidían en que debía haberlos. Fermi había hecho rápidamente uno de sus famosos cálculos, conocidos hoy como problemas de Fermi (¿cuántos pianistas hay en California?), y veía que el resultado chocaba con los datos observacionales. Y formuló su paradoja:
Si la probabilidad de que los haya es tan alta, ¿por qué no los vemos?
Se dice, también, que Leo Szilard estaba presente y respondió:
Ya están entre nosotros, y se llaman húngaros!
* * *Es difícil preguntarse -y más, responder honestamente- sobre lo que no vemos. Hace poco leía una discusión en uno de los
blogs que sigo, y era clarísimo cuánto cambiarían las posturas -y sobre todo, los argumentos absurdos- si se hubiese preguntado por la existencia de extraterrestres.
Pero no siempre es fácil abstraerse de las ideas preconcebidas que tenemos, y tendemos a pensar que lo que no se observa, no existe. Pensar con claridad es difícil cuanto más visceral es el tema, y tal vez por eso fue alguien de afuera quien miró correctamente una imagen como la siguiente:
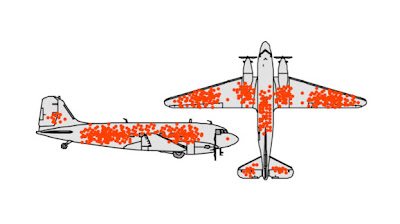
Wald estaba en Columbia, y les cayó como problema analizar el efecto de los impactos en los aviones militares, ya sea para cambiar las tácticas de combate, o para reforzar partes del fuselaje. El
MacTutor dice sólo "
He used his statistical expertise to develop a method to estimate aircraft vulnerability". Si alguien se quiere bancar las cuentas, un análisis sobre su trabajo puede verse en el
JASA (los que no tengan acceso, lo pueden bajar de la página de uno de los autores). También están las casi 100 páginas del original, dando vueltas vía la
wikipedia.
La imagen anterior es de Cameron Moll, Wald recibió tablas de datos, y en su trabajo se ve claramente cómo dividió el avión en sectores y contó los impactos que se observaban en los que volvían de distintas misiones.
La propuesta de Wald, brevemente, fue proteger
más las áreas
menos golpeadas... lo cual puede parecer absurdo, pero no lo es. Su razonamiento era lógico:
Lo que no vemos, justamente, puede ser lo más importante.* * *Los aviones analizados eran los que volvían, pero suponiendo que los impactos se distribuían por igual, eso indicaba que no volvían los aviones que recibían los disparos en las zonas que quedaban con menos marcas.
Las objeciones sobre su suposición son vacías: en la época, sin radares ni métodos de precisión para disparar, con vuelos nocturnos y disparos a ciegas desde las defensas en tierra (basados más en barreras de fuego que en apuntarle a los objetivos), uno esperaría una distribución uniforme de los disparos.
Estadísticamente, se estaba metiendo con los llamados
datos censurados, afectados en este caso por el -muy literal-
survivor bias.
No era el primero, claro: Daniel Bernoulli, doscientos años antes, había incursionado en el tema. Pero esa es ya otra historia.
Post para la Edición 2.1 del Carnaval, esta vez en el blog de su fundador: Tito Eliatron