Hoy iba a escribir un post puteando contra el cientificismo (no contra la ciencia, que no se malentienda), pero como me aceptaron otro paper me cambió el humor (que no las ideas, que tampoco se malentienda). Igual, por ahora no le voy a avisar a mi coautor (tampoco le cambia la vida saberlo o no, aclaremos), que lea el blog y me pregunte si quiere saber (y si no, le digo mañana o pasado).
Encima, me cruzo como 'paper del día' una de esas joyas que en cualquier blog cientificista y/o escéptico destrozarían como pseudociencia, y tiene más material para hacernos reflexionar que en todos los posts que han publicado juntos (je, ya me está volviendo la bronca...) En cualquier momento escribo el post que tenía en mente (me parece).
27.2.06
24.2.06
1095.- Chau, vinistas
21.2.06
1094.- Frases hechas
Es obvio que El Quijote nunca dijo "Elemental, Watson", ni Sherlock Holmes dijo "Ladran, Sancho, señal que cabalgamos". Y aunque parezca raro, tampoco fue al revés.
Y otra cosa rara, como se desprende del paper original (bah, de su traducción) es que Noether nunca mencionó la palabra "simetrías".
Pero ojo, que a diferencia del "todo es relativo" que tampoco dijo Einstein, las simetrías sí van al corazón del teorema de Noether.
Aunque si se mezcla a Einstein con las simetrías, se tiene de golpe la paradoja de los gemelos separados al nacer, uno criado en la tierra y el otro puesto en un cohete que casi a la velocidad de la luz fue y volvió, y cuando se encontraron uno seguía igual y el otro había envejecido. Y es que la paradoja no está en que este fenómeno ocurra -porque se experimentó, no con gemelos [todavía...] pero sí con relojes atómicos-, la paradoja está en la ruptura de la simetría: ¿por qué no envejece el del cohete, si desde su lugar ve que el que se aleja velozmente es la tierra con el otro? La respuesta, acá.
Ah, y como para redondear la idea, la paradoja no es de Einstein, como se suele decir, sino de Langevin, quien la presentó en un congreso de Filosofía en Bologna. Henry Bergson, uno de los presentes, dice que fue esa charla de Langevin la que generó tanto interés de parte de los filósofos por la relatividad.
Bueno, dice..., dicen que dice, digamos.
Y otra cosa rara, como se desprende del paper original (bah, de su traducción) es que Noether nunca mencionó la palabra "simetrías".
Pero ojo, que a diferencia del "todo es relativo" que tampoco dijo Einstein, las simetrías sí van al corazón del teorema de Noether.
Aunque si se mezcla a Einstein con las simetrías, se tiene de golpe la paradoja de los gemelos separados al nacer, uno criado en la tierra y el otro puesto en un cohete que casi a la velocidad de la luz fue y volvió, y cuando se encontraron uno seguía igual y el otro había envejecido. Y es que la paradoja no está en que este fenómeno ocurra -porque se experimentó, no con gemelos [todavía...] pero sí con relojes atómicos-, la paradoja está en la ruptura de la simetría: ¿por qué no envejece el del cohete, si desde su lugar ve que el que se aleja velozmente es la tierra con el otro? La respuesta, acá.
Ah, y como para redondear la idea, la paradoja no es de Einstein, como se suele decir, sino de Langevin, quien la presentó en un congreso de Filosofía en Bologna. Henry Bergson, uno de los presentes, dice que fue esa charla de Langevin la que generó tanto interés de parte de los filósofos por la relatividad.
Bueno, dice..., dicen que dice, digamos.
1093.- Causas y efectos
Parece que la educación está peor de lo que se dice. En España, un alumno le pegó a su docente, y se justificó ante una cámara:
"Me iba a dar una patada, y se la devolví."
"Me iba a dar una patada, y se la devolví."
1092.- Post it
Tanto para postear, que no se por donde empezar. Muchas lecturas, y una semana muy movida en cuestiones de trabajo, y como tampoco sé por donde empezar ahí, mejor vuelvo al blog.
La sorpresa del día (por lo menos para mí): 500 años antes que Leibnitz y Newton, un matemático hindú (Bhaskara II), dijo:
"Bimbaardhasya kotijyaagunastrijyaharaha phalam dorjyayorantaram and Yatra grahasya paramamphalam tatraivagatiphalaabhavena"
no puedo dar fe de que éstas palabras sean las palabras exacatas, que en criollo se traducen como:
"sen(x1)-sen(x0)=(x1 -x0)cos(x0) para x1-x0 chico, y donde el movimiento es máximo, su fruta (la derivada!) es ausente."
La sorpresa del día (por lo menos para mí): 500 años antes que Leibnitz y Newton, un matemático hindú (Bhaskara II), dijo:
"Bimbaardhasya kotijyaagunastrijyaharaha phalam dorjyayorantaram and Yatra grahasya paramamphalam tatraivagatiphalaabhavena"
no puedo dar fe de que éstas palabras sean las palabras exacatas, que en criollo se traducen como:
"sen(x1)-sen(x0)=(x1 -x0)cos(x0) para x1-x0 chico, y donde el movimiento es máximo, su fruta (la derivada!) es ausente."
16.2.06
1091.- Congreso de Futurologia
ese es el título de un cuento de Lem, pero en este caso es una mezcla con la entrega de medallas Field en el ICM'06.
El lenguaje de las apuestas del turf no tiene sentido ya que habrá cuatro medallas (bue, tal vez dejen desierta alguna), pero por costumbre, no está mal:
Favorito: Tao. Bueno, viene desde hace rato, hace unos días LM anunció que es uno de los ganadores, pero lo sacó (ver aquí). Creo que se sabe desde hace dos o tres años, y si no la gana, la propia medalla Field se vería desprestigiada.
Enemigo: Perelman. No es un enemigo de Tao, sino de la Field. Hay un problema grave a resolver con él: todos consideran que su trabajo lleva a la demostración de la conjetura de Poincaré. Si el comité no lo premia, y al día siguiente su trabajo sale en algún journal, ya va a ser demasiado tarde porque habrá superado la barrera de los 40 años y no podrá ganarla jamás. Recordemos que ya se escapó Wiles con su demostración de Fermat... ¿otro más?
Sorpresa: Pujals. Es el único latinoamericano que se me ocurre. Bueno, casi, hay otro pero lo menciono abajo.
Ahora, ¿quiénes más tienen chances reales? D. Gaitsgory, E. Lindenstrauss, y M. Bhargava.
Qué otros nombres se me ocurren? A. C. Ponce, F. Merle, X. Cabré (tiene menos de 40?), de ecuaciones. Todos ellos comparten un coautor: Brezis. Pero ecuaciones no es un área que la Field mire con cariño. Y W. Tucker también se la merece, pero es muy ecuaciones diferenciales más análisis numérico. El demostró que el atractor de Lorenz realmente es un fractal.
Vamos a ver, si se abren apuestas pago...
El lenguaje de las apuestas del turf no tiene sentido ya que habrá cuatro medallas (bue, tal vez dejen desierta alguna), pero por costumbre, no está mal:
Favorito: Tao. Bueno, viene desde hace rato, hace unos días LM anunció que es uno de los ganadores, pero lo sacó (ver aquí). Creo que se sabe desde hace dos o tres años, y si no la gana, la propia medalla Field se vería desprestigiada.
Enemigo: Perelman. No es un enemigo de Tao, sino de la Field. Hay un problema grave a resolver con él: todos consideran que su trabajo lleva a la demostración de la conjetura de Poincaré. Si el comité no lo premia, y al día siguiente su trabajo sale en algún journal, ya va a ser demasiado tarde porque habrá superado la barrera de los 40 años y no podrá ganarla jamás. Recordemos que ya se escapó Wiles con su demostración de Fermat... ¿otro más?
Sorpresa: Pujals. Es el único latinoamericano que se me ocurre. Bueno, casi, hay otro pero lo menciono abajo.
Ahora, ¿quiénes más tienen chances reales? D. Gaitsgory, E. Lindenstrauss, y M. Bhargava.
Qué otros nombres se me ocurren? A. C. Ponce, F. Merle, X. Cabré (tiene menos de 40?), de ecuaciones. Todos ellos comparten un coautor: Brezis. Pero ecuaciones no es un área que la Field mire con cariño. Y W. Tucker también se la merece, pero es muy ecuaciones diferenciales más análisis numérico. El demostró que el atractor de Lorenz realmente es un fractal.
Vamos a ver, si se abren apuestas pago...
15.2.06
1090.- Nius
(La Nación) Serán consensuados los criterios de evaluación.
(yo voto por... no, nada)
(Cornetín) Ciencia: estudio de la revista especializada "Nature". Argentina fue elegida como uno de los referentes de la ciencia
(sabrá leer esta chica Valeria?)
(NotEvenWrong) Hawking se vuelve antrópico.
(escribimos en esta serie de posts, que últimamente no había dicho nada, y que eso no era un chiste de mal gusto; igual ya se veía venir por sus papers anteriores)
(yo voto por... no, nada)
(Cornetín) Ciencia: estudio de la revista especializada "Nature". Argentina fue elegida como uno de los referentes de la ciencia
(sabrá leer esta chica Valeria?)
(NotEvenWrong) Hawking se vuelve antrópico.
(escribimos en esta serie de posts, que últimamente no había dicho nada, y que eso no era un chiste de mal gusto; igual ya se veía venir por sus papers anteriores)
14.2.06
1089.- Firmas digitales
13.2.06
11.2.06
9.2.06
1086.- Sin guglear
Sin guglear, cuál de los siguientes títulos no pertenece a una tesis o paper científico:
Fast diffusion to self-similarity: complete spectrum, long time asymptotics, and numerology
Quantum Pseudo-Telepathy
The Abelian Group Structure on Elliptic Curves Saved My Life!
Can one hear the shape of a drum?
Fast diffusion to self-similarity: complete spectrum, long time asymptotics, and numerology
Quantum Pseudo-Telepathy
The Abelian Group Structure on Elliptic Curves Saved My Life!
Can one hear the shape of a drum?
8.2.06
1085.- Reglas claras
- COMMON COURTESY:
A few Acommon courtesy@ rules apply to this class.
(1) Please try to show up on time.
(2) Please do not leave class early and rustle papers in preparation for leaving before class is dismissed.
(3) Try to stay awake - putting your head down on the desk and going to sleep is very distracting.
(4) Don't read newspapers.
(5) Turn off your Cell Phones and Pagers! [en rojo y formato más grande]
Nunca las había visto tan claras como aquí
7.2.06
1084.- Capo
3.2.06
1083.- Troyanos
Algún día tendría que escribir sobre el problema de los tres cuerpos, pero quería contar algo que me acabo de cruzar casi por accidente.
Dados dos cuerpos de gran masa, hay posiciones donde un tercer cuerpo pequeño se ubicaría en una solución estacionaria, y se movería con el resto del sistema manteniendo su posición. Esas posiciones se las llama puntos lagrangianos, y en nuestro sistema solar se calcularon para Júpiter y el Sol. La idea es que los dos tirones gravitatorios ahí se compensan.
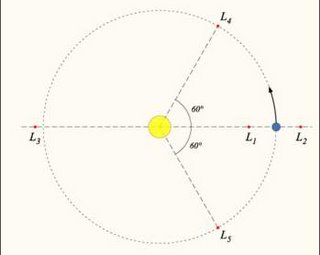
En dos de estos puntos (L4 y L5) hay 'asteroides troyanos'. El nombre se debe a que bautizaron los asteroides con nombres de la Ilíada, a los de L4 con los nombres griegos y a los de L5 con los de los Troyanos.
Y uno se podría preguntar si en estrellas binarias no habría 'planetas troyanos'. Sistemas con dos soles ofrecen muchas posibles órbitas y la de los puntos de Lagrange es una posibilidad interesante. Esta gente forman el único grupo que está explorando eso, y acá tienen una explicación sencilla, y acá una historia de la búsqueda.
Raro, ¿no?
Dados dos cuerpos de gran masa, hay posiciones donde un tercer cuerpo pequeño se ubicaría en una solución estacionaria, y se movería con el resto del sistema manteniendo su posición. Esas posiciones se las llama puntos lagrangianos, y en nuestro sistema solar se calcularon para Júpiter y el Sol. La idea es que los dos tirones gravitatorios ahí se compensan.

En dos de estos puntos (L4 y L5) hay 'asteroides troyanos'. El nombre se debe a que bautizaron los asteroides con nombres de la Ilíada, a los de L4 con los nombres griegos y a los de L5 con los de los Troyanos.
Y uno se podría preguntar si en estrellas binarias no habría 'planetas troyanos'. Sistemas con dos soles ofrecen muchas posibles órbitas y la de los puntos de Lagrange es una posibilidad interesante. Esta gente forman el único grupo que está explorando eso, y acá tienen una explicación sencilla, y acá una historia de la búsqueda.
Raro, ¿no?
2.2.06
1.2.06
1081.- Demostracion por el absurdo (4)
Los siguientes proto intuicionistas fueron Borel y Lebesgue en Francia, y H Weyl en Alemania. De los primeros podemos decir que armaron la moderna teoría de la integral (y que alguien me diga si es muy constructivo / intuitivo el procedimiento... todo muy lindo pero sabemos que es incalculable en la práctica). De Weyl, aparte de que vivió en la Argentina, tendría mucho para decir (mis tesis de licenciatura y de doctorado generalizan resultados suyos de teoría espectral), y lo que conozco de él es poco intuitivo, aunque es cierto que siempre tuvo un ojo mirando hacia las aplicaciones y esto hace que muchos resultados sean 'calculables'.
Y apareció LEJ Brouwer, el holandés que le dio forma al intuicionismo. Sin embargo, es más conocido por sus trabajos en topología (la aproximación simplicial imprescindible en la topología algebraica moderna, el grado topológico que nos permitehallar soluciones probar la existencia de soluciones de ecuaciones diferenciales no lineales, los teoremas de punto fijo...). El fue quien se planteó el tema de qué pasaria si la proposicion: "Si una proposicion no es verdadera, entonces es falsa", no es verdadera, por citar al amigo vqp.
Y apareció LEJ Brouwer, el holandés que le dio forma al intuicionismo. Sin embargo, es más conocido por sus trabajos en topología (la aproximación simplicial imprescindible en la topología algebraica moderna, el grado topológico que nos permite
Suscribirse a:
Comentarios (Atom)
