1323.- Desafio

Ya dije alguna vez que Kac es un capo, y Matías estaba de acuerdo en el apellido pero me cambiaba "Mark" por "Victor" (ver aquí)... ando con ganas de desafiarlo a quién escribe primero un paper citando al otro...

1322.- Dos culturas

Lo malo es que nunca nadie te va a preguntar "¿qué tres teoremas te llevarías a una isla desierta?"

1321.- Predador presa (9)

Pasemos en limpio algunas cosas que hemos visto hasta ahora:

Hasta 1870, los máximos se dan simultáneamente. Recordemos que son capturas, no mediciones directas de la población.

Entre 1870 y 1890, las liebres se comen a los linces.

Después, se comportan como el predador y su presa.

En el mismo período, hay un cambio en el número de manchas solares observadas (aparentemente, las liebres también se comen las manchas solares)

También se han propuesto cambios del modelo:

Amio propuso el tema climático. Ese es un punto que no vi analizado en muchos trabajos de Lotka Volterra, y que debería ser considerado, más aún por sus im/a-plicaciones en estas épocas poco estables en materia climática.

También propuso agregar la presa de la presa (el alimento de la liebre), y me pasó un trabajo donde se estudia el comportamiento caótico del modelo de tres especies.

Y también agregarle difusión, un laplaciano para indicar la migración a zonas con más alimentos / menos predadores.

Julián sugiere cambiar las ecuaciones diferenciales por ecuaciones funcionales, con un delay en la variable temporal (click) que modele la demora en 'enterarse' del crecimiento de la otra especie.

Otras opciones: usar ecuaciones en diferencias (pueden reflejar mejor las finite-size fluctuations); o modelos 'age-structured', donde cada especie se subdivide en dos o tres grupos de edad, cada grupo con sus propias tasas de natalidad, mortalidad, e importancia a la hora de cazar (por ej., las crías no cazan, no se reproducen, y tienen diferente mortalidad que la población total).

No me queda del todo claro que agregar estas cosas explique algo. Tal vez sí, pero sin dudas no va a predecir nada sobre estas poblaciones. La situación de Canadá en el siglo XIX es única, y la combinación de factores político, sociales, y económicos que se dio parece ser única también. Sospecho que una explicación de esos ciclos -que, recordemos, son de pieles de animales cazados, no datos poblacionales- no podrá (no debería) ignorar los puntos del post anterior señalados por Amio.

Entonces... ¿qué nos deja realmente este ejemplo?

1320.- Predador presa (8)

me decía Amio en un primer mail:

Una de las principales hipótesis para las conclusiones sobre el modelo predador-presa a partir de los datos de HBC es que el numero de pieles vendidas a HBC esta correlacionada con la caza y ésta con la población.

Pues no me acabo de creer del todo dicha hipótesis, lo que a mi gusto invalida el resto del análisis.

Tiene toda la razón. Y a continuación desarrolla algunos puntos:

1ro El territorio:

La HBC llegó a tener bajo su monopolio hasta 1870 y con derechos hasta mediados del XX una superficie que casi abarcaba lo que hoy conocemos por Canadá (un casi el 10% de las tierras emergidas del planeta). Asumir que el esfuerzo de caza es constante en dicho territorio a mediados del XIX o despreciar los movimientos de los animales entre zonas con distinto esfuerzo de caza me parece un poco arriesgado. Además poca información tenemos de si las pieles de unos y otros eran cazadas en el mismo lugar.

2do El modo de caza:

Casi todas las capturas eran obtenidas por tramperos. Sería necesario verificar que las trampas eran o no selectivas por especie, qué proporción de animales eran dañados pero no capturados, si era significativa la proporción de liebres que eran devoradas desde que caían en la trampa hasta que era recogida (en algunos tipos de caza esto se ha demostrado especialmente importante).

3ro La importancia de la piel de lince y la liebre para HBC:

Sin menospreciar la exactitud de sus registros parece ser que la HBC compraba muchos tipos de pieles “badger, beaver, bobcat, cougar, coyote, ermine (weasel), fisher, fox, hare, lynx, marten, mink, muskrat, otter, rabbit, raccoon, skunk, squirrel, Wolf, wolverine and even bear", siendo la de castor (beaver) la más importante y siendo las de lince o liebre de una importancia infinitamente menor.

4to Los indios y su peculiar visión del mercado:

La experiencia de NWC (rival de HBC) demuestra que la demanda por parte de los indios de los bienes que como pago en especie ofrecían las empresas de pieles era "inelástica". Los ingleses creían que un incremento en el precio de los productos estimularía un incremento en la caza de pieles hasta que su abundancia en el mercado hiciera descender los precios. Pero cuando los nativos habían ganado lo suficiente para cubrir sus necesidades (no muy amplias) dejaban el comercio. Incluso llegó a ocurrir lo contrario, cuando aumentaban los precios de las pieles, los indígenas necesitaban cazar menos para alcanzar sus necesidades básicas, así que incluso a precios altos las capturas descendían acelerando aún más los problemas de los comerciantes.

Para "ayudar a ajustar la teoría oferta-demanda" hubo de recurrirse a la intimidación, amenaza, secuestro de mujeres y otras lindezas. En palabras de los responsables de la NWC de la época el comercio de pieles era una precarious amalgam of exchanges that ranged from gift to credit transactions, to direct commodity exchanges, to extortion and to theft.

5to Las guerras comerciales y las alianzas:

Esta muy documentado que, en el periodo estudiado, entre las gigantescas corporaciones (sin estado) se establecían tanto terribles guerras comerciales como importantes alianzas. Es especialmente significativo el período de Gobierno de la HBC por parte de George Simpson, (the "Little Emperor,") durante el cual la HBC alcanzó increíbles beneficios a través de control de costes, fidelización de tramperos y de intensa competencia con empresas rivales en las zonas fronterizas de las concesiones. Está documentado que impulsó expediciones a zonas limítrofes con otras empresas para realizar una política de "tierra quemada" para no dejar animales que pudieran atraer a otros tramperos.

También en el periodo de estudio hubo fusión de HBC y NWC. Habría que saber si se fusionaron los registros de capturas ya que entonces el esfuerzo ya no sería constante

7mo La política, las modas y las tendencias en la economía mundial.

La creación en 1870 de Canadá en lo que era el "solar" de las empresas y la apertura del comercio a otras empresas y tramperos es posible que tuviera una gran influencia. Asimismo en el período de estudio distintas modas relacionadas con las pieles fueron yendo y viniendo en Europa.

Seguramente el interés y los incentivos a los tramperos para cazar unas u otras dependía de modas, abundancias relativas, etc. No es de extrañar que las empresas hicieran acopios de pieles antes de sacarlas al mercado (como pasa con la mayor parte de las commodities no perecederas) y solo lo hicieran una vez que los precios fueran altos, haciendo que estos se desplomaran al poco tiempo.

Lo único que se pasó por alto es el punto 6to :P, lo cual en realidad no es muy grave!

Lo que sí es grave, es que estos factores no pueden meterse en las ecuaciones. Son perturbaciones de tipo aleatorio, en gran medida excepcionales, y entran en la ecuación de la población más difícil de modelar: la del verdadero predador, el ser humano.

1319.- Problem(it)a

Se está llevando a cabo una reunión más de la Unión Matemática Argentina, esta vez en Córdoba, y la mayoría de los matemáticos que conozco están allá. Hoy la facultad estaba casi vacía.⁽¹⁾

Así que para postear un problemita bio/bibliográfico, ¿qué matemático tiene 21 Proc. Nat. Acad. USA, 15 Ann. of Math., 11 Bull. AMS, y encima varios papers en las Trans. AMS; Proc. Lond. M.S. y la de Edinb., Comptes Rend., Compositio, Duke, Math. Ann., Math Z., Studia Math., J. d'Analyse Math., JMAA, JDE, Amer. Math. Monthly, Acta Math.... y en la Revista de la UMA?

Pista y anécdota que valía la pena contar: en 1971, un editor le perdió un manuscrito, épocas en que los manuscritos eran manuscritos, y no solía haber un archivo en la computadora porque no solía haber computadoras...

(1) Tomar nota de la nerdidez relacionada con fijar la fecha para tales ausencias congresísticas en coincidencia con el asueto del 21/9. Qué generaciones estaremos (de)formando...

1318.- El diario de Yrigoyen, pero para todos

Ya lo dijo lucas, hace casi dos años y medio, pero no es malo comprobar cada tanto que sigue teniendo razón.

A ver, ¿en qué sección debería salir que las universidades reciben subsidios para proyectos científicos? En ciencia, claro. Bue, no tan claro, que cornetín no tiene una sección de ciencia (ni siquiera un blog, aunque tiene de economía y negocios, videojuegos, pilates...).

Ok, busquemos la de educación... ¿se escribirá con h?, porque así no la veo..., no, parece que tampoco hay. Ah! hay una guía de la educación, que no figura en el índice de la pag. 2, pero tampoco. Ahí no está.

Sospecho que estoy buscando mal, revisemos qué estoy buscando: "las universidades reciben subsidios para proyectos científicos". No! era culpa mía, debería estar buscando "las universidades privadas reciben subsidios para proyectos científicos", si lo quiero encontrar.

Y ahora sí! Después de buscar en la sección PyMes, donde no se ve nada, derechito al suplemento iEco! Nota de cuatro columnas, grafiquito, recuadro... Ahí podemos leer que financiaron 29 proyectos en 11 universidades privadas, entre 40 y 90 lucas c/u (no el lucas de arriba, claro).

De paso, hay más de un dato interesante en la nota para analizar, quedarán para otro post (el sistema de búsqueda es un desastre, así que no esperen que linkee la nota).

ya seguiremos con LV, pa'ciencia

1317.- Predador presa (7)

¿Entonces? Cualquier explicación para el ciclo de 1875-1885 fallará para los ciclos del siglo XX, a menos que la complejidad del modelo correcto sea mucho mayor. Recordemos que en el primer post de esta serie habíamos dicho que era una paradoja que un comportamiento tan simple de las especies diera lugar a un modelo tan complicado como este:

u_t = auv + u (b-u)
v_t = c uv + v (d-v)

Amio me señala por mail otras cuatro variables a considerar:

1ro El ciclo herbivoro. La abundancia de presas para el predador es igual de determinante que la abundancia de alimento para el herbívoro (presa). Las liebres son voraces y su hábitat no es especialmente generoso en “forraje” invernal, además es posible que haya selección sobre plantas con resistencia a ser consumidas por liebres (espinosas, con substancias quimicas repelentes...)

2do Hay más de un predador y mas de una presa. El ciclo pivota en la preferencia del lince por la liebre sobre cualquier otras posible presa, sobre todo cuando esta abunda pero se ha demostrado que en periodos “difíciles” el lince comerá prácticamente cualquier otra cosa, si esta está a su alcance. Además, se ha demostrado que el coyote es mucho más eficaz cazador de liebres que el lince cuando estas están en la parte creciente del ciclo poblacional, el lince es más eficaz cuando la liebre está en retroceso.

3ro El ciclo climático. Los patrones ajustados de temperaturas, precipitaciones, AOI (artic oscillation index), muestran también unos dientes de sierra notables para el periodo de estudio. Es razonable pensar que diferencias de precipitaciones y temperaturas alteraran factores como la producción de alimento para las liebres o los éxitos de las camadas de ambas especies. Además diferencias en temperaturas y precipitaciones pueden alterar las “posibilidades” de la liebre para esconderse (mimetizarse) o del lince para perseguirla (si la nieve es profunda y blanda) y por tanto modificarían la eficiencia de la caza. La interferencia climática podría
explicar porque en determinados experimentos en la región del Yukón, en los que se aportaba alimento artificial a los linces en algunas zonas o se excluían predadores en otras no pudieron modificar el ciclo.

4to Migraciones. Se han registrado movimientos del lince que superan los 1.000 km, así que los descensos en capturas pueden deberse en lugar de a muerte, a migración.

Los puntos 1 y 2 se arreglan "fácil": cada especie extra que uno quiera considerar, agrega una ecuación más de las anteriores, y la variable de la ecuación (u, v, w,...) entra en las otras ecuaciones jugando a favor o en contra según sea un nuevo predador o una nueva presa.

El punto 3 también es "fácil" de arreglar: los coeficientes a, b, c, d pasan a ser variables también. Por ejemplo, b y d representan algo así como las poblaciones de cada especie que el medio puede sostener si no hubiera interacción con las otras, ahora, si las lluvias o la nieve dejan gran parte del territorio inhabitable durante una parte del año, b y d deberían variar de acuerdo a esos factores climáticos.

Por último, 4 también puede tenerse en cuenta "facilmente": es sólo cuestión de agregarle difusión al modelo (para que tenga en cuenta la migración de áreas más pobladas a menos pobladas), y tal vez hasta un término de convección (si consideramos que el clima o la persecusión de los tramperos empuja las poblaciones en determinadas direcciones).

Para convencerlos de la "facilidad" con la que arreglamos las cosas, podemos escribir rápidamente un modelo terminado para n especies considerando estos factores:

u_{1 t} - (d₁(t, x, u₁,...,u_n)u_{1 xx}- c₁(t, x, u₁,...,u_n)u_{1 x} = a₁(u₁,...,u_n)f₁(t, x, u₁,...u_n) + g₁(t, x, u₁)

(y ecuaciones similares para las poblaciones de las otras especies u₂,...u_n). La función f₁ representa el crecimiento o decrecimiento de la población 1 según las otras especies presentes, y la función g₁ representa el crecimiento de la especie 1 en ausencia de las otras [generalizan los términos auv y u(b-u)].

Desde ya, esto no nos dice nada. Deberíamos ser capaces de conocer las funciones d, c, f y g, y aún conociéndolas, deberíamos poder resolver el sistema que queda... Y todavía hay más problemas para considerar.

1316.- Predador presa (6)

Desde ya, Gilpin no creía que las liebres se comían a los linces, así que propuso una explicación para el gráfico del post anterior: las liebres tenían alguna enfermedad que era mortal para los linces que los comían.

Ahora, esto tiene sus problemas: no se conocía ninguna enfermedad tal, ni había signos de linces muertos por alguna peste desconocida, ni se veían linces enfermos paseando por ahí. Gilpin, que de gil sólo tenía la mitad del apellido, propuso que tal vez la enfermedad eran los propios tramperos.

La idea es interesante, y nos recuerda la paradoja de D'Ancona (post 1312) que llevó a Volterra a descubrir las mismas ecuaciones, si bien en este caso hay ciertas diferencias⁽¹⁾.

Razonemos un minuto poniéndonos en el lugar de un trampero.

Observa que la población de liebres está creciendo, son más fáciles de cazar, y pone trampas para liebres, puede cazar muchas.

La población de linces empieza a crecer, y decide entonces cazarlos también.

La población de liebres tiene menos presión de los linces, y se mantiene estable, pero la de linces empieza a disminuir por la caza y porque la de liebres dejó de crecer.

La caza de linces bajó a cierto valor mínimo, y el trampero se concentra en las liebres.

La población de liebres decrece, y el trampero caza pocas pieles de unos y otros.

Ambas poblaciones están reducidas, y el trampero prefiere cazar más linces que liebres otra vez porque las pieles le rinden más.

Liberadas de la presión de los linces, las liebres empiezan a crecer.

Otra vez, el ciclo se repite.

Pero cuidado: este es otro ciclo. No es el del post 1310, donde se
habla del comportamiento de las poblaciones de una presa y su predador, ni el del post 1315, donde se intenta explicar un gráfico 'extraño' suponiendo que el ciclo representa las poblaciones de un predador y su presa.

Aquí, el ciclo obedece a la dificultad (o la comodidad) de atrapar un animal en lugar del otro, suponiendo que en igualdad de condiciones, el predador es más 'atractivo' que su presa para el trampero.

Pero cuidado (otra vez): estamos lejos de poder afirmar que esta es la solución del problema, y si no me creen, vayan mirando el gráfico en la parte del siglo XX...




(1) así como en época de guerra cualquier agujero es trinchera, combinado con que para el hambre no hay pan duro, resulta lógico que los tanos, ante la dificultad de pescar sardinas, se conformaran con comer rayas y tiburones. En cambio, entre una piel de lince y una de liebre, es creíble que sea preferible la del predador antes que la de la presa.

1315.- Predador presa (5)

Las liebres se comen a los linces? (Gilpin, 1973)

Esto puede no ser evidente del gráfico anterior, pero podemos mostrar otro que los convencerá:



Cada punto representa el número de pieles de liebre y de linces capturados cada año (comenzando en 1875), y se ve claramente un ciclo de casi diez años... pero veamos con cuidado el sentido de las flechas:

Luego de un descenso común, el número de liebres sigue bajando mientras que el de linces permanece casi constante.

De golpe, crece el número de linces (!)

cCvio! Si se liberaron de la presión de las liebres que se los comían

El número de liebres comienza a crecer, y el de linces sigue creciendo.

Lójico! hay muchos linces y las liebres consiguen comida fácil!

En el punto (60,80) el crecimiento de la población de linces se frena, y la de liebres sigue creciendo (?)

Porsupu: los linces comienzan a sentir el acoso de las liebres voraces

Cuando el número de liebres está en un máximo, el de linces cae bruscamente.

Claaaro! hay muchas liebres y se están comiendo a todos los linces que encuentran!

y el ciclo debería volver a repetirse...

Las siguientes imágenes muestran a un lince llamando a la liebre para que se lo coma:





(hemos omitido la siguiente imagen de la secuencia, ver al tierno lincecito devorado por esa liebre depravada fue superior a mis fuerzas)

1314.- El cura ajedrecista

Cumplida la cuarta ronda el maestro se ubicaba tranquilamente en el primer lugar. Luego de ganar su partida Velásquez salió a recorrer las calles de la ciudad antes de ir a descansar. Inesperadamente comenzó a llover en forma violenta y buscó algún lugar donde refugiarse; tras caminar algunos pasos divisó una iglesia y se ubicó en su portal.

Mientras esperaba que la lluvia terminara el maestro observó hacia el interior de la iglesia y su sorpresa fue mayúscula cuando vio al sacerdote y su monaguillo jugando una partida de ajedrez. La pasión por el juego es demasiada y el maestro se decidió a golpear la puerta.

Suspendo momentáneamente la serie de Predador-presa para linkear esta hermosa historia que cumple ya dos años en el blog de Sertal.

Leer "el cura ajedrecista".

1313.- Predador presa (4)

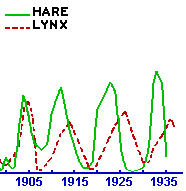
Pero volvamos al gráfico de la Hudson Bay Company:



Hay algo muy extraño en el gráfico, en los años 55, 75, 85, 95, y 05: los máximos se dan en forma casi simultánea, como si el crecimiento en la población de liebres no sólo ayudara a un crecimiento a la par en la población de linces (que podría ser creíble), sino que en el mismo momento en que las liebres comienzan a decrecer, los linces también!

Peor: hay irregularidades más finas, como el pico en 1850 (y en 1881) de las liebres que coincide con un mínimo de los linces; o el crecimiento de los linces entre 1882 y 1887, que se anticipa al crecimiento de las liebres; o los máximos en la población de linces en los años 1895 y 1901 (el máximo de la población de liebres ocurre después, cuando la población de linces está decreciendo).

La explicación "obvia" que se desprende de tales mediciones es muy clara: las liebres se comen a los linces!

1312.- Predador presa (3)

Antes de explicar el gráfico vamos a ver una tabla obtenida unos miles de km más lejos, en los puertos italianos del mediterráneo. En Fiume, por ejemplo, el porcentaje de predadores en el total de los peces atrapados era el siguiente:

1914 1915 1916 1917 1918 1919 1920 1921 1922 1923
12....21....22....21....36....27....16....16....15....11

Estos números, y otros similares, los recogió Umberto D'Ancona en la década del '20. Durante la guerra el número de peces predadores había aumentado -considerando que las capturas eran proporcionales a la población total de peces- lo cual en principio le resultaba bastante lógico: con el Meditarráneo como escenario de maniobras militares, la pesca de sardinas había disminuído; la población de estos peces debía aumentar, lo cual provocaría entonces el aumento de sus predadores... pero revisando la población de los peces 'presa', ésta había disminuido! Aparentemente, la pesca favorecía la a la población de sardinas y similares... vaya uno a saber qué ocurría⁽¹⁾.

Por suerte, Umberto estaba casado con la hija de un matemático, Vito Volterra. Cuando su yerno le planteó el problema, se puso a trabajar en eso y encontró unas ecuaciones similares a las de Lotka. El crecimiento del número de predadores debía influir en la población de presas, y ésta dejar de crecer. Ancona estaba siendo ingenuo al suponer que ambas poblaciones seguirían creciendo.

(1) Al final va a resultar que Bush tenía razón con aquello de talar los bosques para evitar los incendios forestales...

1311.- Predador presa (2)

Desde ya, la paradoja importante no es el modelo. Después de todo, la tendencia a formalizar un hecho obvio es uno de los grandes 'avances' de la matemática del siglo XX...

Pero ni Lotka ni Volterra pertenecían a esa clase de formalistas. Ambos llegaron a sus modelos al encontrar una contradicción con el ciclo que describíamos antes. Según esto, el gráfico de las poblaciones de un predador (lince) y su presa (liebre) debería ser así:



Acá entra en la historia la Hudson Bay Company de Canadá, la corporación comercial más antigua de América del Norte, que se dedicaba a la venta de pieles. Ya en 1831, uno de sus gerentes notó el ciclo en el número de liebres, por lo cual cada diez años aproximadamente los indios no salían a cazarlas -había pocas, y se pasaban todo el día pescando para alimentarse-. La empresa llevaba una estadística detallada de las pieles de liebres y linces vendidas, y suponiendo que la caza es proporcional a la población de animales, permiten afirmar que las poblaciones de animales seguían este ciclo de unos diez años. Veamos los valores:



Estos datos aparecen en casi todos los textos que hablan de las ecuaciones de Lotka Volterra, como un buen ejemplo del ciclo que comentábamos en el post anterior. Pero -y esa es la paradoja- como ejemplo es pésimo! ¿Se ve por qué?

1310.- Predador presa

[Ya hablamos por aquí de Lotka, aunque los posts no están aquí sino en los de zonalibre (archivo de enero de 2005) que todavía no importé, no hablamos de Volterra, quien en paralelo hizo lo mismo que él, y a partir de una paradoja similar: eso es lo que quiero contar.]

Un predador y su presa son un sistema bastante especial. Si la presa se extingue, el predador se morirá de hambre (a menos que tenga otra presa como opción). Si coexisten, se tiene que dar un fenómeno más o menos oscilatorio -o periódico- se repite más o menos lo siguiente:

El predador se come las presas, tiene crías, aumenta su población...

...y el número de presas decrece, están muy perseguidas, son cada vez menos...

...con lo cual al predador le faltan presas para comer, le cuesta conseguir alimentos, la población de predadores decrece, pasan hambre, son cada vez menos...

...y el número de presas crece, no están muy perseguidas, se reproducen, son cada vez más...

...con lo cual el predador se come las presas, tiene crías, aumenta su población...

Y el ciclo vuelve a empezar, un dibujito así:



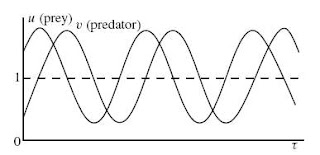
Resumiendo, una tremenda pelotudez que -paradójicamente- no debería haber engendrado nunca un sistema de ecuaciones diferenciales como los que hoy llamamos Lotka-Volterra:

u_t = a uv + u (b-u)
v_t = c uv + v (d-v)

1309.- No recuerdo el autor

-¿Pensarán las máquinas algún día?

-Computo que no.