Dados dos cuerpos de gran masa, hay posiciones donde un tercer cuerpo pequeño se ubicaría en una solución estacionaria, y se movería con el resto del sistema manteniendo su posición. Esas posiciones se las llama puntos lagrangianos, y en nuestro sistema solar se calcularon para Júpiter y el Sol. La idea es que los dos tirones gravitatorios ahí se compensan.
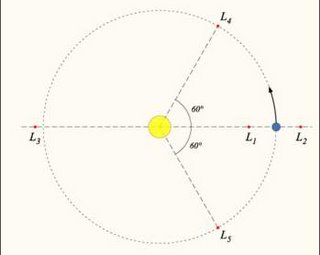
En dos de estos puntos (L4 y L5) hay 'asteroides troyanos'. El nombre se debe a que bautizaron los asteroides con nombres de la Ilíada, a los de L4 con los nombres griegos y a los de L5 con los de los Troyanos.
Y uno se podría preguntar si en estrellas binarias no habría 'planetas troyanos'. Sistemas con dos soles ofrecen muchas posibles órbitas y la de los puntos de Lagrange es una posibilidad interesante. Esta gente forman el único grupo que está explorando eso, y acá tienen una explicación sencilla, y acá una historia de la búsqueda.
Raro, ¿no?
19 comentarios:
Que es lo raro? El metodo, o la idea de planetas que orbiten mas de una estrella, con los enredos orbitales resultantes?
Respecto de lo primero, te dire que esta gente encontro un metodo mas divertido y espectacular.
Que orbiten dos, aparece seguido en scifi (incluso, soles de distintos colores, órbitas 'raras', etc) Acá, la idea me pareció más rara (y entre otras cosas me recordó los satélites geoestacionarios, y algunas cosas más personales, como la última vez que vi un satélite moviéndose por el cielo). Los tipos linkean una enciclopedia de búsquedas, con los distintos grupos y métodos, aquí.
> La idea es que los dos tirones gravitatorios ahí se compensan.
Bueno... pero no es que las fuerzas gravitarias de los dos cuerpos grandes se anulen (cosa que nunca podría ocurrir en L4, L5 que no están sobre la línea que los une). Supongo que sí podría hablarse de una anulación total de fuerzas resultantes si incluimos las pseudo-fuerzas centrígugas y de Coriolis.... ¿no?
Sigue resultándome asombroso que los puntos atractores L4 L5 formen un triángulo equilátero [*], independientemente de las masas de los cuerpos (dentro de un rango).
[* "isosceles triangle (three equal sides and 60O angles)" dice acá. (Isósceles?)]
no, claro que no es que una compense a la otra, sino que ambas se anulan entre sí sumando los efectos de las de rotación. Ahora, por simetría, no corresponde decir que orbiten respecto a uno o al otro, sino que están ahí, como quietos, asociados a ambos.
(El triángulo es equilátero, sí, ahí le pifiaron, o será la curvatura? :P)
Ya que estamos con la gravitacion, una duda que surgio en un almuerzo reciente:
Suponiendo un planeta esferico y de masa homogenea, si hago un pozo hasta el centro de la esfera y me tiro, que pasa?
te quebrás hasta la lengua... diría yo.
No es tan trivial me parece, la aceleracion de la gravedad iria disminuyendo y seria 0 en el centro de la esfera. Aun asi tenemos el "problemita" del momentum acumulado.
Si el pozo llega hasta las antipodas del punto de partida, entonces yo oscilaria alrededor del centro?
> Si el pozo llega hasta las antipodas del punto de partida, entonces yo oscilaria alrededor del centro?
Claro (idealizando, por supuesto:
sin rozamientos, suponiendo masa
uniforme... y temperatura soportable)
quedarías oscilando entre las antípodas, como un resorte. (De hecho, si no equivoco, la ecuación que resulta es exactamente la del resorte ideal: la fuerza gravitaroria es inversamente proporcional al cuadrado de r, pero a su vez la masa de la tierra que tenes abajo -la unica que ejerce atracción- es proporcional a r al cubo, con lo cual la fuerza varía como r; sería interesante -y facil- calcular el período de oscilación).
Y creo recordar (lo mencionaba C. S. Lewis en "The discarded image") la cuestión la habían planteado en la baja edad media, y llegado a la misma respuesta (cualitativamente hablando, claro).
a ver, está claro que estamos idealizando bastante, pero si el pozo es sólo hasta la mitad, me parece que no es cierto que en el centro la fuerza se haga cero. El centro de masa estaría un poco más abajo (hay una columna de tierra que corresponde a la masa que falta en el pozo).
Aún si la gravedad se hiciera cero en ese punto, eso significa que la aceleración se hizo nula, con lo cual, sigue con la velocidad que venía (de ahí que se le hagan polvo hasta las muelas).
Si el orificio sigue de lado a lado, es como dice Hernán (Acá está la derivación completa)
estuve buscando sobre el tema de la edad media, y sólo encontré un artículo de un historiador, Edward Grant, al que no se tiene acceso sin pagar...
Ahí me fijé. Lewis se refiere a
Vincent de Beavouis (Speculum Naturale; siglo 13). Pero, como se ve, si bien el tipo acierta al pensar que el centro sería un punto de equlibrio, no tiene en cuenta la conservación de la energía...
De paso, C. S. Lewis también menciona el que tal vez sea el primer efecto de "ciencia ficción" de la literatura: cuando en la Divina Comedia los viajeros (Dante y Virgilio) bajan al infierno hasta encontrar a Lucifer en el centro de la tierra: al pasar, arrastrándose, por su cintura, en un punto deben dejar de bajar y empezar a subir.
"a su vez la masa de la tierra que tenes abajo -la unica que ejerce atracción- es proporcional a r al cubo"
es asi? entonces, si la tierra fuera hueca, en el interior, la gravedad seria cero?
en esta primera aproximación, sí, porque a grandes rasgos estamos despreciando la distancia, con lo cual la capa de tierra que tenés "encima" se compensa con la que tenés "debajo" por fuera de la bola de radio r (la de los "costados" también se compensan)
Si la tierra fuera hueca, una sola capa y adentro nada, pero una capa lo suficientemente densa, y de un radio muy grande, la gravedad te llevaría hacia las paredes.
me parece que entonces la gravedad resultante seria la gravedad que genera la bola de radio r menos la gravedad que genera la cascara de espesor R-r
pero esa cáscara está tanto por encima como por debajo, no? quiero decir, despreciando las distancias, una compensa la otra y sólo queda el efecto de la bola central
> Si la tierra fuera hueca, una sola capa y adentro nada, pero una capa lo suficientemente densa, y de un radio muy grande, la gravedad te llevaría hacia las paredes.
Ehmmmm me parece (si entendí bien, y si recuerdo bien) que no, creo que un cascarón esférico no ejerce fuerza gravitatoria sobre un punto en su interior (y de no ser así, valdría la objeción de dotuev).
Creo que Newton llegó (trabajosamente) a ese doble resultado, fundamental para su mecánica: por un lado, la fuerza de gravedad de una cáscara esferica uniforme sobre un punto exterior, es equivalente a tener la masa concentrada en el centro; y por otro lado, si el punto está en el interior, es nula.
dos links
que nabo! despreciando las distancias, si no estoy en el centro, la porción de esfera que está "más lejos" también tiene "más masa"!
(traté de deducirlo sin hacer las cuentas, y una vez más "funcionó" mi brillante intuición física... lo imperdonable es que no me acordara de Gauss o Faraday)
(por ésto digo (o ésto, ya que ambas fuerzas matemáticamente son iguales)
Lo de los puntos de Lagrange es muy interesante. Hace un tiempito salió un artículo muy interesante en la Notices AMS. Parece que han indentificado asteroides que tiene una "doble órbita", dan unas vueltas alrededor de Júpiter, y después pasan por el "túnel" en Lagrange y dan algunas vueltas alrededor del sol, y vuelta a empezar. Y lo más interesante es que la matemática del asunto la sacaron de no sé qué de electromagnetismo.
Publicar un comentario