1.- Platón estaba empédocles cuando escribió lo que escribió, si es que lo escribió, la historia es poco creíble, siempre y cuando haya sido bien traducida, y que no sea una modificación posterior de algún traductor o comentador [hay que reconocer que algunas variantes parece haber: estudió todos los números menores a 17? sólo los impares?]. En la línea de los que dudan están Zeuthen y Heath, conocidos historiadores.
2.- Vía congruencias. Martín comenta en el post anterior que llegó hasta el 13 escribiendo n=13q+r. (aunque el tema sea irracionalidad, y no primalidad, este tipo de argumentos me recuerdan el polinomio de Euler, n2+n+41)
3.- En Gaussianos (link al blog a la derecha, junto con los buenos blogs matemáticos), fede esboza la solución de McCabe (Math Magazine 49-4 de 1976, también en la 5ta edición del Hardy - Wright de teoría de números, pag. 42ss.) La idea es mirar los restos al dividir por 2.
4.- La espiral de Teodoro: no hay que despreciar la posibilidad de que Teodoro parara en el 17 porque no lo necesitaba... resulta que una de sus cosas que sí nos llegó es la siguiente espiral:
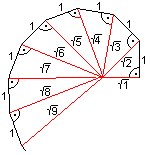
Cada triángulo tiene un ángulo recto, los catetos miden 1 y raíz de n, y la hipotenusa mide raíz de n+1. ¿Qué tiene de interesante aquí el 17? Para 16, se llega a 351 grados y pico, mientras que con 17 se pasa a la vuelta siguiente. ¿Habrá calculado hasta ahí porque era lo que le interesaba para su espiral, y no porque no fuese capaz de demostrarlo para 17?
Vaya uno a saber...
No hay comentarios:
Publicar un comentario