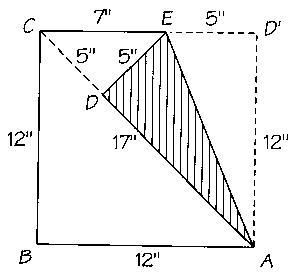
Claro, el 12 y el 17 no tienen nada que ver, la idea es que si raíz de 2 es una fracción a/b, dilatando en b el cuadrado, uno obtendría un cuadrado de lados b, y a es la hipotenusa. Acá no vamos a usar que 2b2=a2, simplemente que con el plegado conseguimos un nuevo cuadradito de lados b-a, es decir, hallamos una fracción con denominador más chico que b. Como el argumento se puede seguir repitiendo, encontramos infinitas fracciones de denominadores cada vez más chicos (y positivos), lo cual no es cierto porque entre 0 y b hay finitos números.
1 comentario:
Aparentemente, esto da una forma de conseguir sucesiones racionales que convergen a raiz de 2:
Se empieza con a/b
y se cambia a/b por (a+2b)/(a+b)
Si por ej. se comienza con 7/5, como en
el dibujo, resulta 17/12, que tambien esta ahi.
Publicar un comentario