25 Greatest Science Books of All-Time es el título de la nota en Discover Magazine que salió mañana(*)
Una de las cosas más extrañas de la lista es el subtítulo "presents the essential reading list for anyone interested in science": no me imagino a nadie para quien resulte esencial la lectura -entre otros- del Philosophiae Naturalis Principia Mathematica de Isaac Newton (1687), ni de la Physica de Aristóteles (circa 330 B.C.), ni del De Humani Corporis Fabrica de Andreas Vesalius (1543), y mucho menos del De Revolutionibus Orbium Coelestium de Copérnico (1543) [tampoco conozco a nadie que haya leído todos estos libros, especialmente el último, que ni siquiera sus contemporáneos lo leyeron!] Sacando algunas partes de los Principia, todos los otros están superados y el contenido que hoy se considera válido de ellos es mínimo (y lo que es válido es tan conocido que no vale la pena ir a leerlo de ahí).
Son -eso sí- grandes hitos de la ciencia que aún desactualizados o superados merecen estar a la par del Origen de las especies de Darwin, los Diálogos sobre dos nuevas ciencias de Galileo, o la Teoría de la relatividad de Einstein (aunque éste sea un libro de divulgación, ya que los trabajos de Einstein fueron publicados como artículos).
Es extraña la presencia de The Voyage of the Beagle de Darwin (1845). En la encuesta que se está haciendo online tiene apenas el 1% de los votos, y eso que está la palanca de figurar primero en la lista.
Lo más extraño de todo es la ausencia de las matemáticas en la lista. Uno, dos tres, infinito del físico Gamow (1947) es una obrita de divulgación no mucho mejor que cualquiera de Gardner, y lejísimo de librazos como What is mathematics de Courant y Robbins, Mathematics and the Imagination, de Kasner y Newman, o Geometry and the Imagination, de Hilbert y Cohn-Vossen.
Y ni hablar de la ausencia de Los Elementos de Euclides... más viejo que cualquiera de los 25 que están en la lista y que los 10 que quedaron afuera, probablemente el primer libro científico del que se tenga noticia y casi tan válido como el primer día!
(*) la magia de la interné, vio?
30.11.06
29.11.06
1219.- Divulgacion cientifica (III)
¿Para qué?
No me gusta el tono utilitarista del '¿para qué?'. Salud, educación, ciencia... ¿para qué? También respecto a hacer guita, acumular poder, pisar cabezas... vale la pregunta: ¿para qué? Podemos preguntar en casi todo ¿para qué?, y podríamos discutir durante horas qué objetivos eran válidos y cuáles no (¿vale hacer divulgación científica para ganar plata? ¿y vale ganar plata para hacer divulgación?)
Sospecho que hay más grises que blancos y negros en todo esto. ¿Está bien pedir un subsidio -fondos públicos, por lo general- para hacer divulgación? Uno puede desentenderse: la plata se pide y que otros decidan si se da o no. ¿Está bien que se otorgue plata para divulgación habiendo a la par pedidos para proyectos de investigación? No hay respuesta fácil, creo que hay que comparar caso por caso, pedido por pedido.
Y, por supuesto, cualquier proyecto / tema / problema de investigación... ¿para qué? Los matemáticos creo que somos los más entrenados en luchar contra esa pregunta, y diría que a la larga aprendemos a mentir bien. No se puede justificar un proyecto de investigación diciendo como Jacobi que
Sin embargo, las respuestas relacionadas con la divulgación suelen venir por ese lado.
Vuelvo a aclarar que no me gusta el tono utilitario de la cosa. Pero no se lo puede ignorar tampoco. Diría que los que crean tener una respuesta clara al ¿para qué? es porque no han participado en una discusión por el reparto de fondos para investigación, ni sobre la función de un docente, o la de un investigador (ni la han presenciado, siquiera). Igual estaría bueno escuchar argumentos nuevos, créanme que hacen falta cada vez más.
(*) La frase empezaba: "It is true that Fourier had the opinion that the principal aim of mathematics was public utility and explanation of natural phenomena; but a philosopher like him should have known that..."
No me gusta el tono utilitarista del '¿para qué?'. Salud, educación, ciencia... ¿para qué? También respecto a hacer guita, acumular poder, pisar cabezas... vale la pregunta: ¿para qué? Podemos preguntar en casi todo ¿para qué?, y podríamos discutir durante horas qué objetivos eran válidos y cuáles no (¿vale hacer divulgación científica para ganar plata? ¿y vale ganar plata para hacer divulgación?)
Sospecho que hay más grises que blancos y negros en todo esto. ¿Está bien pedir un subsidio -fondos públicos, por lo general- para hacer divulgación? Uno puede desentenderse: la plata se pide y que otros decidan si se da o no. ¿Está bien que se otorgue plata para divulgación habiendo a la par pedidos para proyectos de investigación? No hay respuesta fácil, creo que hay que comparar caso por caso, pedido por pedido.
Y, por supuesto, cualquier proyecto / tema / problema de investigación... ¿para qué? Los matemáticos creo que somos los más entrenados en luchar contra esa pregunta, y diría que a la larga aprendemos a mentir bien. No se puede justificar un proyecto de investigación diciendo como Jacobi que
the sole end of science is the honor of the human mind, and that under this title a question about numbers is worth as much as a question about the system of the world.(*)
Sin embargo, las respuestas relacionadas con la divulgación suelen venir por ese lado.
Vuelvo a aclarar que no me gusta el tono utilitario de la cosa. Pero no se lo puede ignorar tampoco. Diría que los que crean tener una respuesta clara al ¿para qué? es porque no han participado en una discusión por el reparto de fondos para investigación, ni sobre la función de un docente, o la de un investigador (ni la han presenciado, siquiera). Igual estaría bueno escuchar argumentos nuevos, créanme que hacen falta cada vez más.
(*) La frase empezaba: "It is true that Fourier had the opinion that the principal aim of mathematics was public utility and explanation of natural phenomena; but a philosopher like him should have known that..."
28.11.06
1218.- Diverge
Si
r= 1 + 1/2 + 1/3 + 1/ 4 + 1/5 + 1/ 6 + ...
= (1 + 1/2) + (1/3 + 1/ 4) + (1/5 + 1/ 6) + ...
> (1/2 + 1/2) + (1/ 4 + 1/ 4) + (1/ 6 + 1/ 6) + ...
= 1 + 1/2 + 1/3 + ...
resulta ser mayor a si mismo: r>r.
La demostración es de la década del '60, de Leonard Gillman; esta entrevista y su continuación tienen buenas anécdotas
r= 1 + 1/2 + 1/3 + 1/ 4 + 1/5 + 1/ 6 + ...
= (1 + 1/2) + (1/3 + 1/ 4) + (1/5 + 1/ 6) + ...
> (1/2 + 1/2) + (1/ 4 + 1/ 4) + (1/ 6 + 1/ 6) + ...
= 1 + 1/2 + 1/3 + ...
resulta ser mayor a si mismo: r>r.
La demostración es de la década del '60, de Leonard Gillman; esta entrevista y su continuación tienen buenas anécdotas
27.11.06
1217.- Divulgacion cientifica (II)
Antes de la divulgación -entendida para el público no científico-, diría que está la difusión. Un resultado tiene que ser conocido primero entre los propios científicos, y no vaya a creer que ese es un problema simple.
Tenemos que retroceder al s.XIX para ver los primeros journals. Antes, los resultados científicos eran transmitidos del maestro a su discípulo, con suerte publicados en planfletos o libros muchas veces pagados por los propios autores, o pasaban de unos a otros por carta. Si pensamos en Copérnico, Kepler, Mersenne, Descartes, Galileo, Huygens, Newton..., vemos que esa fue la forma en que se difundieron sus ideas. Hubo, sí, algunas revistas como el Acta Eruditorum de Leibniz, donde él mismo publicaba con pseudónimos, y durante el s.XVIII se fortalecen las Actas, Proceedings y Transactions de distintas sociedades y academias científicas, que ya venían apareciendo esporádicamente desde el siglo anterior, pero su publicación no era precisamente un modelo de transparencia, seriedad o imparcialidad.
Todavía en el s.XIX uno encuentra que los principales trabajos (la Mecánica de Laplace, la teoría del calor de Fourier, las Disquisitiones de Gauss) se publican como libros. Pero unos pocos años después aparecen un par de journals que siguen hasta el día de hoy: el Journal für die reine und angewandte Mathematik (más conocido como el Journal de Crelle, su fundador) de 1826, y el Journal des Mathematiques Pures et Appliquees, fundado por Liouville en Francia en 1836.(*)
Podemos entender que estuviéramos lejos de frases como:
¿o no?(**)
(*) me pueden acusar, con toda razón, de concentrarme en matemáticas. Ok. Nature empezó a salir en 1869. La química y la biología no siguen patrones muy diferentes en cuanto a la difusión de resultados.
(**) invito, en especial a los saganistas, a encontrar la frase original. Ojo: mi traducción es doblemente mala (incapacidad mía en parte, y en parte a propósito para despistar googliaciones)
Tenemos que retroceder al s.XIX para ver los primeros journals. Antes, los resultados científicos eran transmitidos del maestro a su discípulo, con suerte publicados en planfletos o libros muchas veces pagados por los propios autores, o pasaban de unos a otros por carta. Si pensamos en Copérnico, Kepler, Mersenne, Descartes, Galileo, Huygens, Newton..., vemos que esa fue la forma en que se difundieron sus ideas. Hubo, sí, algunas revistas como el Acta Eruditorum de Leibniz, donde él mismo publicaba con pseudónimos, y durante el s.XVIII se fortalecen las Actas, Proceedings y Transactions de distintas sociedades y academias científicas, que ya venían apareciendo esporádicamente desde el siglo anterior, pero su publicación no era precisamente un modelo de transparencia, seriedad o imparcialidad.
Todavía en el s.XIX uno encuentra que los principales trabajos (la Mecánica de Laplace, la teoría del calor de Fourier, las Disquisitiones de Gauss) se publican como libros. Pero unos pocos años después aparecen un par de journals que siguen hasta el día de hoy: el Journal für die reine und angewandte Mathematik (más conocido como el Journal de Crelle, su fundador) de 1826, y el Journal des Mathematiques Pures et Appliquees, fundado por Liouville en Francia en 1836.(*)
Podemos entender que estuviéramos lejos de frases como:
Entonces, el hombre se vio en un planeta casi imperceptible en la vasta extensión del sistema solar que en sí mismo, es solamente un punto indistinguible en la inmensidad del espacio.
¿o no?(**)
(*) me pueden acusar, con toda razón, de concentrarme en matemáticas. Ok. Nature empezó a salir en 1869. La química y la biología no siguen patrones muy diferentes en cuanto a la difusión de resultados.
(**) invito, en especial a los saganistas, a encontrar la frase original. Ojo: mi traducción es doblemente mala (incapacidad mía en parte, y en parte a propósito para despistar googliaciones)
24.11.06
1216.- Divulgacion cientifica (I)
Ya se que el tema era Sagan, pero voy a empezar por algo actual, esta parte de una entrevista de Arcadi Espasa a Mario Bunge:
¿Quién es Bunge? Mirando en barrapunto, parece que después de estas declaraciones muchos se olvidaron. Pronto lo van a acusar de no ser ateo, de promover la pseudociencia, deenvidioso esto ya está, de irracional esto ya está; es divertido aprender que ser 'de izquierda' o ser 'humanista' implica su irracionalidad; analizar esto podría ser pasto para un post más sobre la irracionalidad, etc.
¿Qué tiene que ver Sagan con esto? Sagan inició esta forma de divulgación científica panfletaria, presentando sus opiniones como científicas. Y encima vendiéndolas, que cada uno tiene derecho a opinar, desde ya, pero no a pretender que uno deba pagar para enterarse.
Va para largo este tema, así que voy a postear otras cosas entre medio. A la entrevista llegué gracias a pseudopodo
-Bueno, ahora que habla de comerse a los curas, ¿qué le parece la cruzada de Dawkins y Dennet contra Dios?
-Bueno, me parece muy bien. Empezó en el siglo XVIII. Lo malo es que ninguno de esos dos propone ciencia auténtica. Toda la genética que usa Dawkins la inventó él. No existe, nada más que en su imaginación.
Mientras lo apuñalaba, iba subrayando que Dawkins era un gran escritor. Cada vez más adentro. Luego añadió.
-Dawkins y Dennet son los dos únicos filósofos millonarios.
¿Quién es Bunge? Mirando en barrapunto, parece que después de estas declaraciones muchos se olvidaron. Pronto lo van a acusar de no ser ateo, de promover la pseudociencia, de
¿Qué tiene que ver Sagan con esto? Sagan inició esta forma de divulgación científica panfletaria, presentando sus opiniones como científicas. Y encima vendiéndolas, que cada uno tiene derecho a opinar, desde ya, pero no a pretender que uno deba pagar para enterarse.
Va para largo este tema, así que voy a postear otras cosas entre medio. A la entrevista llegué gracias a pseudopodo
23.11.06
1215.- Komarov y Gagarin
Gagarín fue el 1er hombre en el espacio (el sputnik y todo eso), y murió joven, apenas 34 años, después de períodos de alcoholimo, en un accidente de aviación. Komarov fue el 1er hombre que muere en el espacio (en el reingreso de la nave), también murió joven.
Claro, uno puede joder y decir que a Komarov le enseñaron a ponerse en órbita pero no a volver:
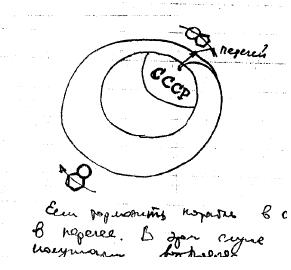
o que Gagarin no entendía muy bien el concepto de límite:

o que estaba más preocupado por el recorrido de las bebidas en su estómago:
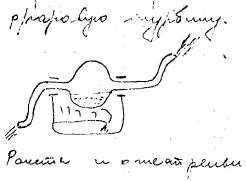
Pero no es mi intención burlarme de estos capos, todo lo contrario. Me resultan admirables, y me alegro de encontrar escaneados y subidos a la red sus Cuadernos, de Gagarin y de Komarov. También hay una carta de algunos astronautas rusos a Brezhnev, analizando la decadencia del programa ruso (en 1965), señalando el incremento de los vuelos no tripulados y el crecimiento del sector misilístico como causas (postura que los yankis imitarían unos años después, con el apoyo de gente como Sagan).
Nada, eso.
Claro, uno puede joder y decir que a Komarov le enseñaron a ponerse en órbita pero no a volver:

o que Gagarin no entendía muy bien el concepto de límite:

o que estaba más preocupado por el recorrido de las bebidas en su estómago:

Pero no es mi intención burlarme de estos capos, todo lo contrario. Me resultan admirables, y me alegro de encontrar escaneados y subidos a la red sus Cuadernos, de Gagarin y de Komarov. También hay una carta de algunos astronautas rusos a Brezhnev, analizando la decadencia del programa ruso (en 1965), señalando el incremento de los vuelos no tripulados y el crecimiento del sector misilístico como causas (postura que los yankis imitarían unos años después, con el apoyo de gente como Sagan).
Nada, eso.
22.11.06
1214.- Pitagoras y Pell
Ya nos convecimos -creo- que no hay solución con números x e y enteros de la ecuación x2 - 2y2=0.
¿Y de x2 - 2y2=1? ¿o igualando a -1?
Resulta que esta fue más fácil de resolver. Por ejemplo, con x=1, y=1 se tiene una solución igualando a -1. Con x=3, y=2 hay una igualando a 1. Ahora x=7, y=5 cumplen 49-2.25=-1
Así, la recursión
xn+1=xn+2yn
yn+1=xn+yn
nos da soluciones para esta ecuación que es un caso particular de la ecuación de Pell (la general es x2 - Dy2=+-1). Matías redescubrió la recursión en este post, pensándolas como aproximaciones de raíz de 2.
Efectivamente, los pitagóricos llamaron a estos números xn, yn
números diagonal y lado [mi traducción es mala: así como llamaban números triangulares y no triángulos, pentagonales y no pentágonos, etc., deberían ser 'diagonaleales' y 'ladeales', ...verdat? {pronúnciase el '...verdat' como Marianitus Grondoneáea}]
Ahora, como xn, yn crecen 'sin cota' (eufesmismo por 'se van al carajo', el tema es que a los griegos no les gustaba mucho el infinito), si uno divide toda la ecuación de Pell por yn2, el +-1 de la derecha se convierte en una cagadésima despreciable, y se obtiene
xn2 / yn2 -2 = cagadésima despreciable
Es decir, los cocientes de xn, yn aproximan raíz de dos.
(Para interesados, este artículo, Pythagorean side and diagonal numbers de László Filep en el Acta Math. Acad. Paed. Nyíregyháziensis 15 (1999) da una versión más seria y detallada del tema, hay versión pedeéfica)
¿Y de x2 - 2y2=1? ¿o igualando a -1?
Resulta que esta fue más fácil de resolver. Por ejemplo, con x=1, y=1 se tiene una solución igualando a -1. Con x=3, y=2 hay una igualando a 1. Ahora x=7, y=5 cumplen 49-2.25=-1
Así, la recursión
xn+1=xn+2yn
yn+1=xn+yn
nos da soluciones para esta ecuación que es un caso particular de la ecuación de Pell (la general es x2 - Dy2=+-1). Matías redescubrió la recursión en este post, pensándolas como aproximaciones de raíz de 2.
Efectivamente, los pitagóricos llamaron a estos números xn, yn
números diagonal y lado [mi traducción es mala: así como llamaban números triangulares y no triángulos, pentagonales y no pentágonos, etc., deberían ser 'diagonaleales' y 'ladeales', ...verdat? {pronúnciase el '...verdat' como Marianitus Grondoneáea}]
Ahora, como xn, yn crecen 'sin cota' (eufesmismo por 'se van al carajo', el tema es que a los griegos no les gustaba mucho el infinito), si uno divide toda la ecuación de Pell por yn2, el +-1 de la derecha se convierte en una cagadésima despreciable, y se obtiene
xn2 / yn2 -2 = cagadésima despreciable
Es decir, los cocientes de xn, yn aproximan raíz de dos.
(Para interesados, este artículo, Pythagorean side and diagonal numbers de László Filep en el Acta Math. Acad. Paed. Nyíregyháziensis 15 (1999) da una versión más seria y detallada del tema, hay versión pedeéfica)
21.11.06
1213.- Predicciones
Vía Hernán, caigo en esta página de chistes científicos y encuentro el siguiente:
Bueno, no. En los ochenta se siguió reduciendo (este paper es de los ochenta). En realidad, Plutón desapareció en agosto de este año.
Cada vez que se ha hecho algun descubrimiento sobre Pluton ha servido para cambiar las estimaciones de su tamaño - y siempre ha disminuido. De hecho, si en los 60 se hubiese hecho una gráfica del tamaño de Pluton contra el tiempo, mostraría claramente que de seguir esa tendencia el planeta iba a desaparecer en los 80.
Bueno, no. En los ochenta se siguió reduciendo (este paper es de los ochenta). En realidad, Plutón desapareció en agosto de este año.
16.11.06
1212.- Ok, ok, es la ultima
La imagen es del Conway-Guy, y confieso que al principio me despistó:
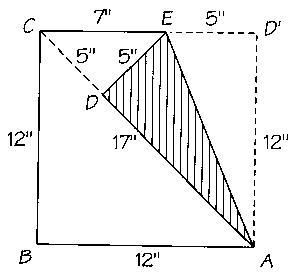
Claro, el 12 y el 17 no tienen nada que ver, la idea es que si raíz de 2 es una fracción a/b, dilatando en b el cuadrado, uno obtendría un cuadrado de lados b, y a es la hipotenusa. Acá no vamos a usar que 2b2=a2, simplemente que con el plegado conseguimos un nuevo cuadradito de lados b-a, es decir, hallamos una fracción con denominador más chico que b. Como el argumento se puede seguir repitiendo, encontramos infinitas fracciones de denominadores cada vez más chicos (y positivos), lo cual no es cierto porque entre 0 y b hay finitos números.

Claro, el 12 y el 17 no tienen nada que ver, la idea es que si raíz de 2 es una fracción a/b, dilatando en b el cuadrado, uno obtendría un cuadrado de lados b, y a es la hipotenusa. Acá no vamos a usar que 2b2=a2, simplemente que con el plegado conseguimos un nuevo cuadradito de lados b-a, es decir, hallamos una fracción con denominador más chico que b. Como el argumento se puede seguir repitiendo, encontramos infinitas fracciones de denominadores cada vez más chicos (y positivos), lo cual no es cierto porque entre 0 y b hay finitos números.
15.11.06
1211.- Analysis by its history
Acabo de terminar el libro de Hairer y Wanner (este). Excelente. Lo leí de un tirón, y en cada hoja encontraba algo nuevo. Me voy a tomar una semanita y lo leo de nuevo. Y con el tiempo, iré posteando algunas de las cosas que encontré.
Por lo pronto, una que nunca había visto en un libro de matemáticas: estereogramas para ilustrar la parte de cálculo en varias variables, dando una impresión de profundidad o 3D.
Por lo pronto, una que nunca había visto en un libro de matemáticas: estereogramas para ilustrar la parte de cálculo en varias variables, dando una impresión de profundidad o 3D.
13.11.06
1210.- Paenza again
El nuevo libro de Adrián Paenza, Matemática estás ahí, episodio 2 está en la calle y también está en la red.
Otra vez, del Depto de Matemáticas de la UBA se puede bajar la versión en pdf, y como la otra vez, les dejo el link para bajarlo: click.
Ahora hay 'menos matemática' y más juegos y problemas de ingenio (je, como si fuesen cosas muy distintas). Mucho material ya circuló por mail, weblogs y demás vía las notas de Página 12. Sospecho que no va a jugarle en contra a las ventas, todo lo contrario. Qué quieren que les diga, más de uno debería seguir el ejemplo de Paenza. Poner el libro gratis en la web no evitó que se convirtiera en un best seller, me animo a decir que todo lo contrario, lo potenció.
Otra vez, del Depto de Matemáticas de la UBA se puede bajar la versión en pdf, y como la otra vez, les dejo el link para bajarlo: click.
Ahora hay 'menos matemática' y más juegos y problemas de ingenio (je, como si fuesen cosas muy distintas). Mucho material ya circuló por mail, weblogs y demás vía las notas de Página 12. Sospecho que no va a jugarle en contra a las ventas, todo lo contrario. Qué quieren que les diga, más de uno debería seguir el ejemplo de Paenza. Poner el libro gratis en la web no evitó que se convirtiera en un best seller, me animo a decir que todo lo contrario, lo potenció.
1209.- Quadratwurzelschnecke
Preguntaba en el post 1199 por la historia de Teodoro mencionada en el Teeteto por Platón, que habría demostrado la irracionalidad de ciertos números hasta el 15, y que no lo hizo para el 17. Hasta el momento, hay varias respuestas:
1.- Platón estaba empédocles cuando escribió lo que escribió, si es que lo escribió, la historia es poco creíble, siempre y cuando haya sido bien traducida, y que no sea una modificación posterior de algún traductor o comentador [hay que reconocer que algunas variantes parece haber: estudió todos los números menores a 17? sólo los impares?]. En la línea de los que dudan están Zeuthen y Heath, conocidos historiadores.
2.- Vía congruencias. Martín comenta en el post anterior que llegó hasta el 13 escribiendo n=13q+r. (aunque el tema sea irracionalidad, y no primalidad, este tipo de argumentos me recuerdan el polinomio de Euler, n2+n+41)
3.- En Gaussianos (link al blog a la derecha, junto con los buenos blogs matemáticos), fede esboza la solución de McCabe (Math Magazine 49-4 de 1976, también en la 5ta edición del Hardy - Wright de teoría de números, pag. 42ss.) La idea es mirar los restos al dividir por 2.
4.- La espiral de Teodoro: no hay que despreciar la posibilidad de que Teodoro parara en el 17 porque no lo necesitaba... resulta que una de sus cosas que sí nos llegó es la siguiente espiral:
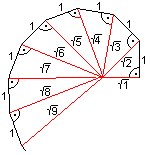
Cada triángulo tiene un ángulo recto, los catetos miden 1 y raíz de n, y la hipotenusa mide raíz de n+1. ¿Qué tiene de interesante aquí el 17? Para 16, se llega a 351 grados y pico, mientras que con 17 se pasa a la vuelta siguiente. ¿Habrá calculado hasta ahí porque era lo que le interesaba para su espiral, y no porque no fuese capaz de demostrarlo para 17?
Vaya uno a saber...
1.- Platón estaba empédocles cuando escribió lo que escribió, si es que lo escribió, la historia es poco creíble, siempre y cuando haya sido bien traducida, y que no sea una modificación posterior de algún traductor o comentador [hay que reconocer que algunas variantes parece haber: estudió todos los números menores a 17? sólo los impares?]. En la línea de los que dudan están Zeuthen y Heath, conocidos historiadores.
2.- Vía congruencias. Martín comenta en el post anterior que llegó hasta el 13 escribiendo n=13q+r. (aunque el tema sea irracionalidad, y no primalidad, este tipo de argumentos me recuerdan el polinomio de Euler, n2+n+41)
3.- En Gaussianos (link al blog a la derecha, junto con los buenos blogs matemáticos), fede esboza la solución de McCabe (Math Magazine 49-4 de 1976, también en la 5ta edición del Hardy - Wright de teoría de números, pag. 42ss.) La idea es mirar los restos al dividir por 2.
4.- La espiral de Teodoro: no hay que despreciar la posibilidad de que Teodoro parara en el 17 porque no lo necesitaba... resulta que una de sus cosas que sí nos llegó es la siguiente espiral:

Cada triángulo tiene un ángulo recto, los catetos miden 1 y raíz de n, y la hipotenusa mide raíz de n+1. ¿Qué tiene de interesante aquí el 17? Para 16, se llega a 351 grados y pico, mientras que con 17 se pasa a la vuelta siguiente. ¿Habrá calculado hasta ahí porque era lo que le interesaba para su espiral, y no porque no fuese capaz de demostrarlo para 17?
Vaya uno a saber...
9.11.06
1208.- Problem(it)a
Dos matemáticos están mirando un polinomio en un pizarrón,
f(x) = anxn +...+ a1x + a0
donde no conocen los coeficientes ak, que son números enteros, ni el grado n.
-A ver, supongamos que la edad de mi hijo es una raíz.
-¿Era 7...?
-No, es más grande. Digamos que f(7)=77.
-A ver, probemos con un número más grande, la edad de mi hija..., ¿qué tal si ahí da 85? ¿Tu mi hijo es más grande que mi hija, no?
-Si, y ahora con esos datos cualquiera puede saber qué edades tienen.
-Listo, preguntemos eso en el parcial, en vez del grado, los coeficientes, y esas boludeces de siempre.
Este problema tiene como 50 años, y no doy la fuente porque no la conozco. En internet aparece en una lista de historia de la matemática en el '97, y en 2000 alguien lo usa en un artículo de educación matemática sin citar nada.
donde no conocen los coeficientes ak, que son números enteros, ni el grado n.
-A ver, supongamos que la edad de mi hijo es una raíz.
-¿Era 7...?
-No, es más grande. Digamos que f(7)=77.
-A ver, probemos con un número más grande, la edad de mi hija..., ¿qué tal si ahí da 85? ¿Tu mi hijo es más grande que mi hija, no?
-Si, y ahora con esos datos cualquiera puede saber qué edades tienen.
-Listo, preguntemos eso en el parcial, en vez del grado, los coeficientes, y esas boludeces de siempre.
Este problema tiene como 50 años, y no doy la fuente porque no la conozco. En internet aparece en una lista de historia de la matemática en el '97, y en 2000 alguien lo usa en un artículo de educación matemática sin citar nada.
8.11.06
1207.- Ahora de numeros otra vez
Si, ya nos convencimos de que raíz de dos es irracional, pero ahí va otra: si es a/b,
a2=2b2
y del lado izquierdo hay un número par de divisores, mientras que en el derecho son impares.
Upgrade 1207.1: me señala Hernán -con mucha razón- que en vez de divisores debería decir factores primos.
y del lado izquierdo hay un número par de divisores, mientras que en el derecho son impares.
Upgrade 1207.1: me señala Hernán -con mucha razón- que en vez de divisores debería decir factores primos.
7.11.06
1206.- Otra clase de irracionalidad
(Nada que ver con todo lo anterior) Esto es por el artículo de Eleanor Robson, Iraq: the history of mathematics and the aftermath of war, British Society for the History of Mathematics Newsletter 49 (2003), 1-9.
Otra historia similar: un tanque voló el frente de la Academia de Ciencias de Irak, para sacar la bandera... tras eso, el 80 por ciento de los 58000 libros y los 2000 manuscritos que había fueron robados.
The Awqaf, established in 1920, held some 7,000 manuscripts, mostly religious, but also including important early scientific works. Staff managed to move most of the collection to safety before the war, sending about a quarter of it, mostly comprising recently acquired material, under armed guard to a mosque. But when one of those guards was shot and killed by US troops on 14 April and the others disarmed, it was decided that the collection would be safer in the Awqaf building after all. That afternoon the library was set upon by organised looters, who stole 22 of the 32 trunks containing the returned manuscripts and then set fire to the building with flammable agents. The whole structure burned to the ground within quarter of an hour; an estimated 700 manuscripts were destroyed in the blaze and a further thousand or so looted.
Otra historia similar: un tanque voló el frente de la Academia de Ciencias de Irak, para sacar la bandera... tras eso, el 80 por ciento de los 58000 libros y los 2000 manuscritos que había fueron robados.
6.11.06
1205.- Logicas ilogicas
Venía dando vueltas sobre el tema de la irracionalidad porque muchas veces algo se califica de irracional pero sin especificar en relación a qué.
En aritmética, irracional no apunta a un número que escapa de la razón (un número inexplicable, o absurdo, o imposible, o que no entra en la cabeza...), sino a uno que no puede representarse como un cociente -o razón- de cantidades enteras.
De la misma manera, que un pensamiento, deducción, creencia, etc. sea irracional está asociado en nuestra cultura a la lógica aristotélica. Tenemos tan arraigado esto que hasta hace unos cien años nadie se cuestionó que podía haber diferentes lógicas, y si esto ocurrió, fue más por culpa de Cantor y su introducción de los distintos infinitos que por otra cosa.
Se quejaba en un comment Osvaldo que por cambiar algún postulado de la lógica clásica no es cuestión de llamar irracional a estas nuevas lógicas, lógicas ilógicas en el sentido tradicional, pero matemáticamente interesantes.
Uno de los intentos más interesantes acepta cierto grado de inconsistencia, para lo cual se deja de lado el principio del 3ro excluído y el ex contradictione quodlibet (de una contradicción se deduce cualquier cosa).
Para mas info al respecto, Inconsistent mathematics, en la Enciclopedia de Filosofía de Stanford. Su autor, Chris Mortensen, escribió un libro sobre el tema que comenta Baez aquí. También, un par de link con laburos actuales en el tema: WoPalo, y artículos; y la entrada de la Wikipedia sobre lógicas paraconsistentes.
En aritmética, irracional no apunta a un número que escapa de la razón (un número inexplicable, o absurdo, o imposible, o que no entra en la cabeza...), sino a uno que no puede representarse como un cociente -o razón- de cantidades enteras.
De la misma manera, que un pensamiento, deducción, creencia, etc. sea irracional está asociado en nuestra cultura a la lógica aristotélica. Tenemos tan arraigado esto que hasta hace unos cien años nadie se cuestionó que podía haber diferentes lógicas, y si esto ocurrió, fue más por culpa de Cantor y su introducción de los distintos infinitos que por otra cosa.
Se quejaba en un comment Osvaldo que por cambiar algún postulado de la lógica clásica no es cuestión de llamar irracional a estas nuevas lógicas, lógicas ilógicas en el sentido tradicional, pero matemáticamente interesantes.
Uno de los intentos más interesantes acepta cierto grado de inconsistencia, para lo cual se deja de lado el principio del 3ro excluído y el ex contradictione quodlibet (de una contradicción se deduce cualquier cosa).
Para mas info al respecto, Inconsistent mathematics, en la Enciclopedia de Filosofía de Stanford. Su autor, Chris Mortensen, escribió un libro sobre el tema que comenta Baez aquí. También, un par de link con laburos actuales en el tema: WoPalo, y artículos; y la entrada de la Wikipedia sobre lógicas paraconsistentes.
3.11.06
1204.- El paper Nature de la semana
Se merece el lugar destacado el paper sobre "The DNA sequence and biological annotation of human chromosome 1".
Pero ojo, no el paper "The DNA sequence and biological annotation of human chromosome 1", que se publicó en mayo, sino el que se publicó el jueves 26 de octubre:
"Corregidendum: The DNA sequence and biological annotation of human chromosome 1", Nature 443.
¿En qué le pifiaron? Se olvidaron de incluír 13 coautores... Esperemos que los 3.141 genes, 991 pseudogenes, y las many coding sequences estén todas bien anotaditas y no se hayan olvidado de incluír nada.
(vía improbable research)
Pero ojo, no el paper "The DNA sequence and biological annotation of human chromosome 1", que se publicó en mayo, sino el que se publicó el jueves 26 de octubre:
"Corregidendum: The DNA sequence and biological annotation of human chromosome 1", Nature 443.
¿En qué le pifiaron? Se olvidaron de incluír 13 coautores... Esperemos que los 3.141 genes, 991 pseudogenes, y las many coding sequences estén todas bien anotaditas y no se hayan olvidado de incluír nada.
(vía improbable research)
1203.- Deducciones irracionales
Escribiendo el post anterior, caigo en la cuenta que Baez (éste) le está contestando (conscientemente o no) a los Sokal-istas cuando defienden:
(Sokal aclara en su paper que vive en un piso 22).
Estaremos de acuerdo que la ciencia no es una mera convención social, pero aún creyendo eso, nadie saca a partir de allí deducciones tan absurdas como para que se contradigan abiertamente con la realidad. Hay un límite en la realidad para la aplicabilidad de la tablita de verdad.
Y un tema aparte es la cantidad de factores a considerar en un problema de corte menos exacto, como para poder distinguir claramente cuál es la hipótesis errónea que lleva a un absurdo. Estoy seguro que diferentes hipótesis, todas razonables consideradas por separado, pueden llevar a conclusiones absurdas interactuando todas juntas... me parece que el campo de la economía es el lugar correcto para buscar ejemplos.
Upgrade 1203.1: siguiendo el consejo de dotuev, aclaremos que la cosa no es con Sokal, sino con sus seguidores, que muchas veces son más papistas que el Papa.
los que crean que la ciencia es una mera convención social, prueben transgredirla tirándose por mi ventana
(Sokal aclara en su paper que vive en un piso 22).
Estaremos de acuerdo que la ciencia no es una mera convención social, pero aún creyendo eso, nadie saca a partir de allí deducciones tan absurdas como para que se contradigan abiertamente con la realidad. Hay un límite en la realidad para la aplicabilidad de la tablita de verdad.
Y un tema aparte es la cantidad de factores a considerar en un problema de corte menos exacto, como para poder distinguir claramente cuál es la hipótesis errónea que lleva a un absurdo. Estoy seguro que diferentes hipótesis, todas razonables consideradas por separado, pueden llevar a conclusiones absurdas interactuando todas juntas... me parece que el campo de la economía es el lugar correcto para buscar ejemplos.
Upgrade 1203.1: siguiendo el consejo de dotuev, aclaremos que la cosa no es con Sokal, sino con sus seguidores, que muchas veces son más papistas que el Papa.
2.11.06
1202.- Mas irracionalidades (pero no de numeros)
Una de esas leyes lógicas que todos sabemos es la de que un resultado falso implica cualquier cosa. En realidad, es una línea en la tabla de verdad de las implicaciones, si p es falso y p implica q, p implica q es verdadero aunque q sea cualquier banana.
Circula una anécdota -que Smullyan atribuye a Russell, otros a Hardy- según la cual alguien -a veces un filósofo, otras gente común, nunca uno de ciencias- se muestra escéptico al respecto -che! que el escepticismo tiene un límite... con ciertas cosas no se jode- y le pide que demuestre que si 1=2, Russell y el Papa son la misma persona. Como él y el Papa son dos personas, pero ya que él es uno, y uno es igual a dos, él es el Papa, argumenta Russell, y el otro se cae'e culo y ve la Luz1. Igual, esta parte no suele estar muy detallada en la anécdota, pero parece que lo convence porque si el otro hubiese dado una réplica interesante, figuraría.
Una réplica interesante la dió Baez varias décadas después: si en una cadena de razonamientos uno llega a un resultado falso o que contradice lo que creemos, lo normal es que uno no salte por la ventana porque eso implica que uno puede volar.
Y los matemáticos lo sabemos bien: cuando llegamos a una contradicción, uno se frena, y en lugar de declarar que vale todo, retrocede buscando dónde estuvo la falla (algún error humano en la deducción) o qué suposición que uno hizo es demasiado atrevida para descartarla (apelando al ppio. del 3ro excluído)2.
Pero todo eso parte de una suposición previa, y es que la premisa es verdadera ó falsa. La cosa se complica cuando uno rechaza esto y entra en las lógicas multivaluadas, donde una proposición A puede ser:
-verdadera, falsa, o indecidible.
-verdadera (1), falsa (0), ó p, con p entre 0 y 1 (fuzzy, probabilidades).
-1, 0, ó n valores extras (Lucasiewicz y Tarski)
Pero todo se pone realmente irracional si uno acepta:
-verdadera, falsa, ó ambas.
(Continuará... O no, o ambas cosas)
(1) es lógico que si queda de espaldas en el suelo vea la Luz, porque esta suele venir de arriba, ya sea el sol, un foco, etc.
(2) ya habíamos hablado del ppio. del 3ro excluído con la excusa de las demostraciones por el absurdo acá, acá y acá
Circula una anécdota -que Smullyan atribuye a Russell, otros a Hardy- según la cual alguien -a veces un filósofo, otras gente común, nunca uno de ciencias- se muestra escéptico al respecto -che! que el escepticismo tiene un límite... con ciertas cosas no se jode- y le pide que demuestre que si 1=2, Russell y el Papa son la misma persona. Como él y el Papa son dos personas, pero ya que él es uno, y uno es igual a dos, él es el Papa, argumenta Russell, y el otro se cae'e culo y ve la Luz1. Igual, esta parte no suele estar muy detallada en la anécdota, pero parece que lo convence porque si el otro hubiese dado una réplica interesante, figuraría.
Una réplica interesante la dió Baez varias décadas después: si en una cadena de razonamientos uno llega a un resultado falso o que contradice lo que creemos, lo normal es que uno no salte por la ventana porque eso implica que uno puede volar.
Y los matemáticos lo sabemos bien: cuando llegamos a una contradicción, uno se frena, y en lugar de declarar que vale todo, retrocede buscando dónde estuvo la falla (algún error humano en la deducción) o qué suposición que uno hizo es demasiado atrevida para descartarla (apelando al ppio. del 3ro excluído)2.
Pero todo eso parte de una suposición previa, y es que la premisa es verdadera ó falsa. La cosa se complica cuando uno rechaza esto y entra en las lógicas multivaluadas, donde una proposición A puede ser:
-verdadera, falsa, o indecidible.
-verdadera (1), falsa (0), ó p, con p entre 0 y 1 (fuzzy, probabilidades).
-1, 0, ó n valores extras (Lucasiewicz y Tarski)
Pero todo se pone realmente irracional si uno acepta:
-verdadera, falsa, ó ambas.
(Continuará... O no, o ambas cosas)
(1) es lógico que si queda de espaldas en el suelo vea la Luz, porque esta suele venir de arriba, ya sea el sol, un foco, etc.
(2) ya habíamos hablado del ppio. del 3ro excluído con la excusa de las demostraciones por el absurdo acá, acá y acá
1.11.06
1201.- Irracionales (II)
Y antes de meterme con cosas realmente irracionales, otra demostración sencilla y fácil de recordar, que utiliza sólo la definición de logaritmo: log2(3) es irracional. Veamos:
Si log2(3)=a/b con a, b enteros,
2(a/b)=3, o sea
2a=3b,
lo cual no puede ser porque un lado es múltiplo exclusivamente de 2 y el otro de 3.
No es difícil demostrar en la misma línea que si m no es una potencia de n, entonces logn(m) no puede ser racional.
Y sobre la irracionalidad en general, pero en otro tema, les recomiendo este excelente post de Alejandro. Pensaba dejarle un comment, pero mejor lo incluyo acá: can I ask if mathematics is 'rational'? (that is, self-consistent or non-contradictory)
lo cual no puede ser porque un lado es múltiplo exclusivamente de 2 y el otro de 3.
No es difícil demostrar en la misma línea que si m no es una potencia de n, entonces logn(m) no puede ser racional.
Y sobre la irracionalidad en general, pero en otro tema, les recomiendo este excelente post de Alejandro. Pensaba dejarle un comment, pero mejor lo incluyo acá: can I ask if mathematics is 'rational'? (that is, self-consistent or non-contradictory)
Suscribirse a:
Comentarios (Atom)