Les cuento cómo llegué al que considero uno de los mejores posts del año: creí que el tema de raíz de dos estaba terminado después de argumentar que la hipotenusa del triángulo rectángulo medía dos. Pero entonces me vino a la mente un post anterior sobre la fórmula del área del triángulo equilátero de Gerberto (que fuera Papa no es un detalle menor en esta historia), y en los comments Hernán -como buen tomista- argumentaba que entendía si era el triángulo rectángulo y no el equilátero...
La aparente contradicción se resolvía afirmando ¡que el triángulo rectángulo era equilátero! Pero si posteaba eso iban a pensar que -siguiendo los consejos de Mr. X- me fumé algo para llegar a esa conclusión, pero no es así, es apenas una cuestión filosófico-histórica sencilla.
Las ideas del atomismo de Demócrito eran conocidas en la edad Media, y también las paradojas de Zenón (al menos, la versión resumida aristotélica) lo cual acarreaba serias dificultades lógicas que enfrentaron los teólogos de las distintas religiones. Siendo discreta la materia (y por ende, el cuerpo humano) cómo se movían los espíritus de un lado a otro era un problema que se encuentra incluso en la Summa de Santo Tomás. Y de ahí a revisar la teología islámica y judía había un paso, sólo era cuestión de escarbar un poco en las obras de Maimónides, Ibn Ezra y Avicena para hallar la respuesta.
El post Teologías, atomismo, y la longitud de la diagonal del cuadrado unitario mide uno fue el resultado, y tuvo entonces muy poco de original, apenas el trabajo de mezclar los datos para ver que a esta conclusión ya se había llegado mil años atrás.
29.12.06
28.12.06
1235.- Balance (III)
¿Y los peores posts? ¿Por qué no?
Año deportivo éste que va terminando: los hubo sobre el mundial de futbol (Italia-Ghana, Inglaterra y Trinidad y Tobago), y después con el de matemáticas (el anuncio, fields 1, fields 2, estadísticas auxiliares).
Hubo también posts serios y malísimos como el homenaje a mis inclasificables lectores, o el teléfono descompuesto.
Y también posts menos reflexivos pero igual de malos, como el hoax o qué sobre el NA-TMA (que, entre paréntesis, apareció el autor del paper en los comments!), el problema propuesto por G. Martínez, o las discusiones sobre las demostraciones por el absurdo, la irracionalidad, y el principio antrópico (en cada caso, se pueden rastrear los posts previos del tema).
Año deportivo éste que va terminando: los hubo sobre el mundial de futbol (Italia-Ghana, Inglaterra y Trinidad y Tobago), y después con el de matemáticas (el anuncio, fields 1, fields 2, estadísticas auxiliares).
Hubo también posts serios y malísimos como el homenaje a mis inclasificables lectores, o el teléfono descompuesto.
Y también posts menos reflexivos pero igual de malos, como el hoax o qué sobre el NA-TMA (que, entre paréntesis, apareció el autor del paper en los comments!), el problema propuesto por G. Martínez, o las discusiones sobre las demostraciones por el absurdo, la irracionalidad, y el principio antrópico (en cada caso, se pueden rastrear los posts previos del tema).
27.12.06
1234.- Balance (II)
Otro post del que me siento más que orgulloso fue Ptolomeus ab omni naevo vindicatus.
Lamento que algunos imbéciles en los comments me hayan acusado de geocéntrico, egocéntrico, y hasta de oge, goe, eog y oeg-céntrico, pero repito: la gracia del modelo ptolemaico es que es precisamente un modelo matemático, independiente de la realidad, detalle del cual el propio Ptolomeo era consciente.
Lamento que algunos imbéciles en los comments me hayan acusado de geocéntrico, egocéntrico, y hasta de oge, goe, eog y oeg-céntrico, pero repito: la gracia del modelo ptolemaico es que es precisamente un modelo matemático, independiente de la realidad, detalle del cual el propio Ptolomeo era consciente.
26.12.06
1233.- Balance
Este es el quinto fin de año con el blog, y nunca hice un balance de los mejores posts del año ni nada similar. Pero es lo que voy a hacer esta semana: un post por día entre el 26 y el 30 con los que considero mis mejores posts del 2006.
El primer post es la lista de los libros científicos que publiqué a propuesta de pseudópodo en éste otro post. Por supuesto, no llegué a 25, pero no era la idea. Mi criterio fue privilegiar la calidad sobre la cantidad (y él tampoco llegó a 25 en su lista, sólo 14, pero realmente muy recomendables!).
El primer post es la lista de los libros científicos que publiqué a propuesta de pseudópodo en éste otro post. Por supuesto, no llegué a 25, pero no era la idea. Mi criterio fue privilegiar la calidad sobre la cantidad (y él tampoco llegó a 25 en su lista, sólo 14, pero realmente muy recomendables!).
22.12.06
1232.- Felices Fiestas
Feliz Navidad y Año Nuevo! Que pasen todos muy felices fiestas, con sus flías/amigos!
y no pierdan tiempo leyendo las 133 páginas del último volumen del Annales de Physique, disfruten en vivo y en directo de la Nucléation, ascension et éclatement d'une bulle de champagne, ya que como dice el abstract, since the time of the benedictine monk dom Pierre Perignon (1638-1715), champagne is the wine of celebration. This fame is largely linked to the elegance of its effervescence and foaming properties. Salud!
y no pierdan tiempo leyendo las 133 páginas del último volumen del Annales de Physique, disfruten en vivo y en directo de la Nucléation, ascension et éclatement d'une bulle de champagne, ya que como dice el abstract, since the time of the benedictine monk dom Pierre Perignon (1638-1715), champagne is the wine of celebration. This fame is largely linked to the elegance of its effervescence and foaming properties. Salud!
21.12.06
1231.- Euler formula
Si anotáramos todas las fórmulas de Euler, llenaríamos varios libros. Si hasta la zeta de Riemann le debemos...
Retrocedamos: en sus últimos años de vida, la mitad de las publicaciones de la Academia de Ciencias de San Petersburgo eran textos suyos, y dejó una pila de trabajos que se siguieron publicando después a ese mismo ritmo (durante 20 años, si mal no recuerdo). Por costumbre, las distintas fórmulas de Euler fueron recibiendo el nombre del primero que las usó, o el siguiente que las publicó.
Pero como decíamos en el post 1129, está el Principio de Arnold, y si lo aplicamos a las conocidas fórmula e identidad de Euler, encontramos lo siguiente:
-que la identidad de Euler ex+iy=ex(cos(y)+isen(y)), se debe a Roger Cotes que la encontró primero
-y que la fórmula V - E + F = 2, donde V, E, F se lee 'número de vértices, lados y caras', la encontró nada menos que Descartes.
Retrocedamos: en sus últimos años de vida, la mitad de las publicaciones de la Academia de Ciencias de San Petersburgo eran textos suyos, y dejó una pila de trabajos que se siguieron publicando después a ese mismo ritmo (durante 20 años, si mal no recuerdo). Por costumbre, las distintas fórmulas de Euler fueron recibiendo el nombre del primero que las usó, o el siguiente que las publicó.
Pero como decíamos en el post 1129, está el Principio de Arnold, y si lo aplicamos a las conocidas fórmula e identidad de Euler, encontramos lo siguiente:
-que la identidad de Euler ex+iy=ex(cos(y)+isen(y)), se debe a Roger Cotes que la encontró primero
-y que la fórmula V - E + F = 2, donde V, E, F se lee 'número de vértices, lados y caras', la encontró nada menos que Descartes.
20.12.06
1230.- Algo para ver
Alemania-Grecia, en el Estadio Olimpico de Munchen (audio en alemán, así que una transcripción en inglés no viene mal), gracias a Nothing but Flowers
19.12.06
1229.- La paradoja de Schwarz
Hoy viene complicado el día para ampliar lo del post anterior, pero voy a mencionar un fenómeno que no por repetido deja de sorprenderme:
-La paradoja de Schwarz la descubrió Peano
Todo bien, total Peano pasó a la historia de por vida gracias a los axiomas del número natural, aunque
-Los axiomas del número natural los propuso Dedekind
Claramente, estamos frente a ejemplos claros del Principio de Arnold:
-Si una noción matemática merece llevar el nombre de una persona, entonces éste no es el nombre de quien la descubrió.
El Principio de Arnold fue formulado por Sir Michael Berry.
-La paradoja de Schwarz la descubrió Peano
Todo bien, total Peano pasó a la historia de por vida gracias a los axiomas del número natural, aunque
-Los axiomas del número natural los propuso Dedekind
Claramente, estamos frente a ejemplos claros del Principio de Arnold:
-Si una noción matemática merece llevar el nombre de una persona, entonces éste no es el nombre de quien la descubrió.
El Principio de Arnold fue formulado por Sir Michael Berry.
18.12.06
1228.- Ultimo momento
Olvídense de los posts 1207, 1212, 1214. Evidentemente, la longitud de la diagonal del cuadrado unitario es 2, basta seguir la línea azul:

Y si tomamos cubitos más chicos, vemos que siempre la escalerita que aproxima la diagonal mide 2.
(gráfico afanated from Taxi cab geometry, pero ese no es el tema, lo que tenía en mente era la paradoja de Schwarz, que en realidad tampoco es de él, sino de Peano. Ampliaremos)

Y si tomamos cubitos más chicos, vemos que siempre la escalerita que aproxima la diagonal mide 2.
(gráfico afanated from Taxi cab geometry, pero ese no es el tema, lo que tenía en mente era la paradoja de Schwarz, que en realidad tampoco es de él, sino de Peano. Ampliaremos)
15.12.06
1227.- Sinceridad
Cuando me preguntan en qué trabajo, una buena respuesta es problemas de autovalores y vibraciones para materiales pseudoplásticos o dilatantes y fluidos no newtonianos gobernados por el p-laplaciano.
Traducción: monstruitos de maizena.
(más videos en cornstarch y en nonnewtonian)
13.12.06
1226.- Universidades TICs web 2.0
son palabras que en google devuelven una bocha de resultados de todo el mundo.
Ahora, si queremos hablar en serio de internet2 o Redes Académicas y Científicas de Prestaciones Avanzadas en el país, vamos a encontrar también unas cuantas expresiones de deseo, festejos cuando se lanzaron los proyectos, etc...
Aunque hoy que se cumplen justo 5 años de la primer conexión de las universidades argentinas a Internet2 (ver aquí, por ejemplo), no se ven festejos por ningún lado: es que hay noticias que no se difunden tanto, como que la Argentina ahora quedó afuera de la Red Mundial de Investigación y Desarrollo por no pagar los 300 mil dólares de la conexión (la nota está en las univ. nac. del Litoral y del Sur).
[Hace una semana apareció cierta publicación, cuyo prólogo denuncia "Miopía e involución en el sistema universitario argentino", itálicas mías. Je... nunca ví un texto que se desactualizara más rápido. ]
[Por si alguien piensa que lo que pasó está restringido a las universidades, también quedaron afuera la CNEA y el Servicio Meteorológico]
Ahora, si queremos hablar en serio de internet2 o Redes Académicas y Científicas de Prestaciones Avanzadas en el país, vamos a encontrar también unas cuantas expresiones de deseo, festejos cuando se lanzaron los proyectos, etc...
Aunque hoy que se cumplen justo 5 años de la primer conexión de las universidades argentinas a Internet2 (ver aquí, por ejemplo), no se ven festejos por ningún lado: es que hay noticias que no se difunden tanto, como que la Argentina ahora quedó afuera de la Red Mundial de Investigación y Desarrollo por no pagar los 300 mil dólares de la conexión (la nota está en las univ. nac. del Litoral y del Sur).
[Hace una semana apareció cierta publicación, cuyo prólogo denuncia "Miopía e involución en el sistema universitario argentino", itálicas mías. Je... nunca ví un texto que se desactualizara más rápido. ]
[Por si alguien piensa que lo que pasó está restringido a las universidades, también quedaron afuera la CNEA y el Servicio Meteorológico]
11.12.06
1225.- Gerberto
Escribe Cajori que escribe Hermann Hankel:
Cosa'e locos 1) la carta puede llegar a estar online si se copan y la escanean (y capaz que está, si uno busca mejor). Y estamos hablando de una carta de más de mil años.
Cosa'e locos 2) Gerberto es más conocido como el Papa Silvestre II (999-1003), y entre otras cosas, tradujo y corrigió la geometría de Boecio, agregándole resultados nuevos.
Cosa'e locos 3) La formulita del área del triángulo no está en ninguna parte de los Elementos de Euclides.
el primer trabajo matemático de la Edad Media que merece ese nombre es una carta de Gerberto a Adalbold, el obispo de Utrecht, en la cual explicaba la razón por la cual el área de un triángulo, obtenida "geométricamente" como el producto de la base por la mitad de la altura, difería de la calculada "aritméticamente" de acuerdo a la fórmula a(a+1)/2, utilizada por los topógrafos, donde a es el lado de un triángulo equilátero. Dio la explicación correcta de que en la última fórmula se cuentan todos los pequeños cuadrados en los cuales se divide el triángulo, pero que algunos se prolongan fuera de él.
Cosa'e locos 1) la carta puede llegar a estar online si se copan y la escanean (y capaz que está, si uno busca mejor). Y estamos hablando de una carta de más de mil años.
Cosa'e locos 2) Gerberto es más conocido como el Papa Silvestre II (999-1003), y entre otras cosas, tradujo y corrigió la geometría de Boecio, agregándole resultados nuevos.
Cosa'e locos 3) La formulita del área del triángulo no está en ninguna parte de los Elementos de Euclides.
6.12.06
1224.- Cuestion de fe
Todo conocimiento científico descansa en una evaluación razonable de la probabilidad, al concitar consenso y oposición. Pensemos, por ejemplo, en la construcción del mundo estelar en la astronomía, o en las leyes de la herencia y las ideas evolucionistas en la biología, todos ellos resultados que hoy consideramos como verdades seguras y comprobadas. Sería el fin de la ciencia y la imposibilidad de cualquier progreso el que ni siquiera admitiéramos como verdades las leyes de la aritmética elemental. Y sin embargo, aún en nuestros días hay seguidores de Kronecker que ponen en duda el principio del tercero excluído.
David Hilbert, Fundamentos de las matemáticas, (pag 126)
5.12.06
1223.- Este es un post a pedido
de Ramiro que dice que me guglió pero no encontró ningún post hablando de Magic Squares / Cuadrados Mágicos salvo en una referencia al grabado de Albercht Durer "Melancolia".
Mi mail / post respuesta:
Y ahora, algo más grave. ¿Vieron que tampoco hablé nunca del sudoku? La única regularidad que descubrí es la misma del S como autovalor, consecuencia también de Markov. ¿Alguien se prende y hacemos algo más serio?
Mi mail / post respuesta:
es cierto, nunca hablé de eso y confieso por qué: los consideraba una pérdida de tiempo, una boludez sin contenido matemático 'real' ni mayor interés que ubicar numeritos para que filas/columnas sumen lo mismo...
...hasta que se me ocurrió considerarlos como matrices, y como a tales, buscarles sus autovalores.
Resultado, que encontré con matlab que existían siempre autovalores: el valor de la suma S de cada fila/columna estaba; salvo ese, si estaba A estaba -A; y en los pares 0 era autovalor. Tratando de demostrar eso, vi que dividiendo por S era una matriz doblemente estocástica, y como los valores eran positivos, de Markov (eso explicaba que S fuera autovalor), etc. Eso los metía de cabeza dentro de una teoría más o menos bien conocida, y con propiedades de toda clase. Si hubiese pensado antes en eso, podría haber publicado algo al respecto, de hecho ya hay un paper que prueba menos de lo que digo ahí arriba.
Moraleja: muchas cosas son una boludez hasta que se las mira desde el ángulo adecuado, y en ese momento nos pueden hacer quedar como boludos a nosotros.
Y ahora, algo más grave. ¿Vieron que tampoco hablé nunca del sudoku? La única regularidad que descubrí es la misma del S como autovalor, consecuencia también de Markov. ¿Alguien se prende y hacemos algo más serio?
4.12.06
1222.- El paper Nature del año
...es el mismo del año pasado de Science, y no es un paper, sino una editorial.
Responding to fraud es una editorial sobre el resultado de un año de investigación sobre cómo se publicaron los dos papers de clonación de células madres. La investigación está disponible acá con una breve respuesta de Science.
En breve, dice: no hicimos nada mal, el sistema de referato funcionó, no fue culpa nuestra; el único cambio a futuro es que cuando digan que prueban un resultado "unexpected and/or counterintuitive, or touch on areas of high political controversy" les vamos a prestar mayor atención y tomar algunas medidas. "These might include higher standards for including primary data, demands for clearer specification of the roles of all authors, and more intensive evaluation of the treatment of digital images."
Me asombra la 'criminalización' a priori de las ideas nuevas, el juzgarlas con mayor severidad por "unexpected and/or counterintuitive". Sobre todo, porque en este caso no era ese el problema, no era un paper que viniera por fuera de la 'ciencia normal' -à la Kuhn-, todo lo contrario.
Lo absurdo de esta medida es que justamente en las áreas controversiales o un resultado "unexpected and/or counterintuitive" suele estar sometido a mayor contrastación y si había algo raro se suele descubrir. Justamente, son los papers pertenecientes al paradigma dominante los que son publicados sin muchas vueltas, no los "unexpected and/or counterintuitive" (si no me creen, revisen el historial de rechazos que suelen tener los ganadores de Nobels... antes de ganar el premio, claro).
Me suena que la respuesta no estuvo a la altura de las circunstancias. Como lavada de manos parece muy buena, que "dentro de Science" fueron vilmente engañados y a cualquiera le hubiera podido pasar. Pero quedaron detalles sin mencionar en el reporte que van de "Science para afuera" tales como: la imagen de que se puede colar fácil un resultado, la falla del peer-review que es más profunda de lo que reconocen (la falsabilidad de los resultados a cierto nivel es imposible), y el verdadero impacto del trabajo -de lo cual deberían hacerse cargo, ya que están orgullosos de tener el 2do Impact Factor más alto del mundo, y es de esperar que el trabajo se difunda y se cite a otro ritmo-.
Responding to fraud es una editorial sobre el resultado de un año de investigación sobre cómo se publicaron los dos papers de clonación de células madres. La investigación está disponible acá con una breve respuesta de Science.
En breve, dice: no hicimos nada mal, el sistema de referato funcionó, no fue culpa nuestra; el único cambio a futuro es que cuando digan que prueban un resultado "unexpected and/or counterintuitive, or touch on areas of high political controversy" les vamos a prestar mayor atención y tomar algunas medidas. "These might include higher standards for including primary data, demands for clearer specification of the roles of all authors, and more intensive evaluation of the treatment of digital images."
Me asombra la 'criminalización' a priori de las ideas nuevas, el juzgarlas con mayor severidad por "unexpected and/or counterintuitive". Sobre todo, porque en este caso no era ese el problema, no era un paper que viniera por fuera de la 'ciencia normal' -à la Kuhn-, todo lo contrario.
Lo absurdo de esta medida es que justamente en las áreas controversiales o un resultado "unexpected and/or counterintuitive" suele estar sometido a mayor contrastación y si había algo raro se suele descubrir. Justamente, son los papers pertenecientes al paradigma dominante los que son publicados sin muchas vueltas, no los "unexpected and/or counterintuitive" (si no me creen, revisen el historial de rechazos que suelen tener los ganadores de Nobels... antes de ganar el premio, claro).
Me suena que la respuesta no estuvo a la altura de las circunstancias. Como lavada de manos parece muy buena, que "dentro de Science" fueron vilmente engañados y a cualquiera le hubiera podido pasar. Pero quedaron detalles sin mencionar en el reporte que van de "Science para afuera" tales como: la imagen de que se puede colar fácil un resultado, la falla del peer-review que es más profunda de lo que reconocen (la falsabilidad de los resultados a cierto nivel es imposible), y el verdadero impacto del trabajo -de lo cual deberían hacerse cargo, ya que están orgullosos de tener el 2do Impact Factor más alto del mundo, y es de esperar que el trabajo se difunda y se cite a otro ritmo-.
2.12.06
1221.- Problem(it)a
-...es que no puedo decir eso en la clase si no hice la cuenta, mirá si alguno descubre que es un error.
-Y hacela, entonces!
-Pero me da fiaca! Ponerme a contar cuántos números menores a 216000 escritos en base 60 no tienen ningún cero...
-Dale, si es fácil, pensalo como 593, bue..., 216 mil menos eso. Casi diez mil, ponele. Menos del 2 por ciento.
-Claaa...aro, pero eso es para los de tres dígitos..., no, ni en pedo hago la cuenta. Y encima después tengo que ver cuántos en base 10 tienen algún cero, y comprobar que son casi la mitad.
-Hacé una cosa, postealo con alguna pista de cómo encarar la cuenta y alguno la va a terminar, yo sé que les tenés confianza. A todo esto, ¿para qué tanto lío?
-No, nada, parece que en Babilonia no tenían un símbolo para el cero por ese motivo, porque no lo necesitaban ya que deducían del contexto en los casos que hubiera hecho falta.
-Ah, ¿y no trabajaban con números más grandes? ¿Ni los astrónomos?
-Justamente, ellos sí tenían un símbolo para el cero, pero los matemáticos no!
-Y hacela, entonces!
-Pero me da fiaca! Ponerme a contar cuántos números menores a 216000 escritos en base 60 no tienen ningún cero...
-Dale, si es fácil, pensalo como 593, bue..., 216 mil menos eso. Casi diez mil, ponele. Menos del 2 por ciento.
-Claaa...aro, pero eso es para los de tres dígitos..., no, ni en pedo hago la cuenta. Y encima después tengo que ver cuántos en base 10 tienen algún cero, y comprobar que son casi la mitad.
-Hacé una cosa, postealo con alguna pista de cómo encarar la cuenta y alguno la va a terminar, yo sé que les tenés confianza. A todo esto, ¿para qué tanto lío?
-No, nada, parece que en Babilonia no tenían un símbolo para el cero por ese motivo, porque no lo necesitaban ya que deducían del contexto en los casos que hubiera hecho falta.
-Ah, ¿y no trabajaban con números más grandes? ¿Ni los astrónomos?
-Justamente, ellos sí tenían un símbolo para el cero, pero los matemáticos no!
30.11.06
1220.- Discover y los grandes libros de la ciencia
25 Greatest Science Books of All-Time es el título de la nota en Discover Magazine que salió mañana(*)
Una de las cosas más extrañas de la lista es el subtítulo "presents the essential reading list for anyone interested in science": no me imagino a nadie para quien resulte esencial la lectura -entre otros- del Philosophiae Naturalis Principia Mathematica de Isaac Newton (1687), ni de la Physica de Aristóteles (circa 330 B.C.), ni del De Humani Corporis Fabrica de Andreas Vesalius (1543), y mucho menos del De Revolutionibus Orbium Coelestium de Copérnico (1543) [tampoco conozco a nadie que haya leído todos estos libros, especialmente el último, que ni siquiera sus contemporáneos lo leyeron!] Sacando algunas partes de los Principia, todos los otros están superados y el contenido que hoy se considera válido de ellos es mínimo (y lo que es válido es tan conocido que no vale la pena ir a leerlo de ahí).
Son -eso sí- grandes hitos de la ciencia que aún desactualizados o superados merecen estar a la par del Origen de las especies de Darwin, los Diálogos sobre dos nuevas ciencias de Galileo, o la Teoría de la relatividad de Einstein (aunque éste sea un libro de divulgación, ya que los trabajos de Einstein fueron publicados como artículos).
Es extraña la presencia de The Voyage of the Beagle de Darwin (1845). En la encuesta que se está haciendo online tiene apenas el 1% de los votos, y eso que está la palanca de figurar primero en la lista.
Lo más extraño de todo es la ausencia de las matemáticas en la lista. Uno, dos tres, infinito del físico Gamow (1947) es una obrita de divulgación no mucho mejor que cualquiera de Gardner, y lejísimo de librazos como What is mathematics de Courant y Robbins, Mathematics and the Imagination, de Kasner y Newman, o Geometry and the Imagination, de Hilbert y Cohn-Vossen.
Y ni hablar de la ausencia de Los Elementos de Euclides... más viejo que cualquiera de los 25 que están en la lista y que los 10 que quedaron afuera, probablemente el primer libro científico del que se tenga noticia y casi tan válido como el primer día!
(*) la magia de la interné, vio?
Una de las cosas más extrañas de la lista es el subtítulo "presents the essential reading list for anyone interested in science": no me imagino a nadie para quien resulte esencial la lectura -entre otros- del Philosophiae Naturalis Principia Mathematica de Isaac Newton (1687), ni de la Physica de Aristóteles (circa 330 B.C.), ni del De Humani Corporis Fabrica de Andreas Vesalius (1543), y mucho menos del De Revolutionibus Orbium Coelestium de Copérnico (1543) [tampoco conozco a nadie que haya leído todos estos libros, especialmente el último, que ni siquiera sus contemporáneos lo leyeron!] Sacando algunas partes de los Principia, todos los otros están superados y el contenido que hoy se considera válido de ellos es mínimo (y lo que es válido es tan conocido que no vale la pena ir a leerlo de ahí).
Son -eso sí- grandes hitos de la ciencia que aún desactualizados o superados merecen estar a la par del Origen de las especies de Darwin, los Diálogos sobre dos nuevas ciencias de Galileo, o la Teoría de la relatividad de Einstein (aunque éste sea un libro de divulgación, ya que los trabajos de Einstein fueron publicados como artículos).
Es extraña la presencia de The Voyage of the Beagle de Darwin (1845). En la encuesta que se está haciendo online tiene apenas el 1% de los votos, y eso que está la palanca de figurar primero en la lista.
Lo más extraño de todo es la ausencia de las matemáticas en la lista. Uno, dos tres, infinito del físico Gamow (1947) es una obrita de divulgación no mucho mejor que cualquiera de Gardner, y lejísimo de librazos como What is mathematics de Courant y Robbins, Mathematics and the Imagination, de Kasner y Newman, o Geometry and the Imagination, de Hilbert y Cohn-Vossen.
Y ni hablar de la ausencia de Los Elementos de Euclides... más viejo que cualquiera de los 25 que están en la lista y que los 10 que quedaron afuera, probablemente el primer libro científico del que se tenga noticia y casi tan válido como el primer día!
(*) la magia de la interné, vio?
29.11.06
1219.- Divulgacion cientifica (III)
¿Para qué?
No me gusta el tono utilitarista del '¿para qué?'. Salud, educación, ciencia... ¿para qué? También respecto a hacer guita, acumular poder, pisar cabezas... vale la pregunta: ¿para qué? Podemos preguntar en casi todo ¿para qué?, y podríamos discutir durante horas qué objetivos eran válidos y cuáles no (¿vale hacer divulgación científica para ganar plata? ¿y vale ganar plata para hacer divulgación?)
Sospecho que hay más grises que blancos y negros en todo esto. ¿Está bien pedir un subsidio -fondos públicos, por lo general- para hacer divulgación? Uno puede desentenderse: la plata se pide y que otros decidan si se da o no. ¿Está bien que se otorgue plata para divulgación habiendo a la par pedidos para proyectos de investigación? No hay respuesta fácil, creo que hay que comparar caso por caso, pedido por pedido.
Y, por supuesto, cualquier proyecto / tema / problema de investigación... ¿para qué? Los matemáticos creo que somos los más entrenados en luchar contra esa pregunta, y diría que a la larga aprendemos a mentir bien. No se puede justificar un proyecto de investigación diciendo como Jacobi que
Sin embargo, las respuestas relacionadas con la divulgación suelen venir por ese lado.
Vuelvo a aclarar que no me gusta el tono utilitario de la cosa. Pero no se lo puede ignorar tampoco. Diría que los que crean tener una respuesta clara al ¿para qué? es porque no han participado en una discusión por el reparto de fondos para investigación, ni sobre la función de un docente, o la de un investigador (ni la han presenciado, siquiera). Igual estaría bueno escuchar argumentos nuevos, créanme que hacen falta cada vez más.
(*) La frase empezaba: "It is true that Fourier had the opinion that the principal aim of mathematics was public utility and explanation of natural phenomena; but a philosopher like him should have known that..."
No me gusta el tono utilitarista del '¿para qué?'. Salud, educación, ciencia... ¿para qué? También respecto a hacer guita, acumular poder, pisar cabezas... vale la pregunta: ¿para qué? Podemos preguntar en casi todo ¿para qué?, y podríamos discutir durante horas qué objetivos eran válidos y cuáles no (¿vale hacer divulgación científica para ganar plata? ¿y vale ganar plata para hacer divulgación?)
Sospecho que hay más grises que blancos y negros en todo esto. ¿Está bien pedir un subsidio -fondos públicos, por lo general- para hacer divulgación? Uno puede desentenderse: la plata se pide y que otros decidan si se da o no. ¿Está bien que se otorgue plata para divulgación habiendo a la par pedidos para proyectos de investigación? No hay respuesta fácil, creo que hay que comparar caso por caso, pedido por pedido.
Y, por supuesto, cualquier proyecto / tema / problema de investigación... ¿para qué? Los matemáticos creo que somos los más entrenados en luchar contra esa pregunta, y diría que a la larga aprendemos a mentir bien. No se puede justificar un proyecto de investigación diciendo como Jacobi que
the sole end of science is the honor of the human mind, and that under this title a question about numbers is worth as much as a question about the system of the world.(*)
Sin embargo, las respuestas relacionadas con la divulgación suelen venir por ese lado.
Vuelvo a aclarar que no me gusta el tono utilitario de la cosa. Pero no se lo puede ignorar tampoco. Diría que los que crean tener una respuesta clara al ¿para qué? es porque no han participado en una discusión por el reparto de fondos para investigación, ni sobre la función de un docente, o la de un investigador (ni la han presenciado, siquiera). Igual estaría bueno escuchar argumentos nuevos, créanme que hacen falta cada vez más.
(*) La frase empezaba: "It is true that Fourier had the opinion that the principal aim of mathematics was public utility and explanation of natural phenomena; but a philosopher like him should have known that..."
28.11.06
1218.- Diverge
Si
r= 1 + 1/2 + 1/3 + 1/ 4 + 1/5 + 1/ 6 + ...
= (1 + 1/2) + (1/3 + 1/ 4) + (1/5 + 1/ 6) + ...
> (1/2 + 1/2) + (1/ 4 + 1/ 4) + (1/ 6 + 1/ 6) + ...
= 1 + 1/2 + 1/3 + ...
resulta ser mayor a si mismo: r>r.
La demostración es de la década del '60, de Leonard Gillman; esta entrevista y su continuación tienen buenas anécdotas
r= 1 + 1/2 + 1/3 + 1/ 4 + 1/5 + 1/ 6 + ...
= (1 + 1/2) + (1/3 + 1/ 4) + (1/5 + 1/ 6) + ...
> (1/2 + 1/2) + (1/ 4 + 1/ 4) + (1/ 6 + 1/ 6) + ...
= 1 + 1/2 + 1/3 + ...
resulta ser mayor a si mismo: r>r.
La demostración es de la década del '60, de Leonard Gillman; esta entrevista y su continuación tienen buenas anécdotas
27.11.06
1217.- Divulgacion cientifica (II)
Antes de la divulgación -entendida para el público no científico-, diría que está la difusión. Un resultado tiene que ser conocido primero entre los propios científicos, y no vaya a creer que ese es un problema simple.
Tenemos que retroceder al s.XIX para ver los primeros journals. Antes, los resultados científicos eran transmitidos del maestro a su discípulo, con suerte publicados en planfletos o libros muchas veces pagados por los propios autores, o pasaban de unos a otros por carta. Si pensamos en Copérnico, Kepler, Mersenne, Descartes, Galileo, Huygens, Newton..., vemos que esa fue la forma en que se difundieron sus ideas. Hubo, sí, algunas revistas como el Acta Eruditorum de Leibniz, donde él mismo publicaba con pseudónimos, y durante el s.XVIII se fortalecen las Actas, Proceedings y Transactions de distintas sociedades y academias científicas, que ya venían apareciendo esporádicamente desde el siglo anterior, pero su publicación no era precisamente un modelo de transparencia, seriedad o imparcialidad.
Todavía en el s.XIX uno encuentra que los principales trabajos (la Mecánica de Laplace, la teoría del calor de Fourier, las Disquisitiones de Gauss) se publican como libros. Pero unos pocos años después aparecen un par de journals que siguen hasta el día de hoy: el Journal für die reine und angewandte Mathematik (más conocido como el Journal de Crelle, su fundador) de 1826, y el Journal des Mathematiques Pures et Appliquees, fundado por Liouville en Francia en 1836.(*)
Podemos entender que estuviéramos lejos de frases como:
¿o no?(**)
(*) me pueden acusar, con toda razón, de concentrarme en matemáticas. Ok. Nature empezó a salir en 1869. La química y la biología no siguen patrones muy diferentes en cuanto a la difusión de resultados.
(**) invito, en especial a los saganistas, a encontrar la frase original. Ojo: mi traducción es doblemente mala (incapacidad mía en parte, y en parte a propósito para despistar googliaciones)
Tenemos que retroceder al s.XIX para ver los primeros journals. Antes, los resultados científicos eran transmitidos del maestro a su discípulo, con suerte publicados en planfletos o libros muchas veces pagados por los propios autores, o pasaban de unos a otros por carta. Si pensamos en Copérnico, Kepler, Mersenne, Descartes, Galileo, Huygens, Newton..., vemos que esa fue la forma en que se difundieron sus ideas. Hubo, sí, algunas revistas como el Acta Eruditorum de Leibniz, donde él mismo publicaba con pseudónimos, y durante el s.XVIII se fortalecen las Actas, Proceedings y Transactions de distintas sociedades y academias científicas, que ya venían apareciendo esporádicamente desde el siglo anterior, pero su publicación no era precisamente un modelo de transparencia, seriedad o imparcialidad.
Todavía en el s.XIX uno encuentra que los principales trabajos (la Mecánica de Laplace, la teoría del calor de Fourier, las Disquisitiones de Gauss) se publican como libros. Pero unos pocos años después aparecen un par de journals que siguen hasta el día de hoy: el Journal für die reine und angewandte Mathematik (más conocido como el Journal de Crelle, su fundador) de 1826, y el Journal des Mathematiques Pures et Appliquees, fundado por Liouville en Francia en 1836.(*)
Podemos entender que estuviéramos lejos de frases como:
Entonces, el hombre se vio en un planeta casi imperceptible en la vasta extensión del sistema solar que en sí mismo, es solamente un punto indistinguible en la inmensidad del espacio.
¿o no?(**)
(*) me pueden acusar, con toda razón, de concentrarme en matemáticas. Ok. Nature empezó a salir en 1869. La química y la biología no siguen patrones muy diferentes en cuanto a la difusión de resultados.
(**) invito, en especial a los saganistas, a encontrar la frase original. Ojo: mi traducción es doblemente mala (incapacidad mía en parte, y en parte a propósito para despistar googliaciones)
24.11.06
1216.- Divulgacion cientifica (I)
Ya se que el tema era Sagan, pero voy a empezar por algo actual, esta parte de una entrevista de Arcadi Espasa a Mario Bunge:
¿Quién es Bunge? Mirando en barrapunto, parece que después de estas declaraciones muchos se olvidaron. Pronto lo van a acusar de no ser ateo, de promover la pseudociencia, deenvidioso esto ya está, de irracional esto ya está; es divertido aprender que ser 'de izquierda' o ser 'humanista' implica su irracionalidad; analizar esto podría ser pasto para un post más sobre la irracionalidad, etc.
¿Qué tiene que ver Sagan con esto? Sagan inició esta forma de divulgación científica panfletaria, presentando sus opiniones como científicas. Y encima vendiéndolas, que cada uno tiene derecho a opinar, desde ya, pero no a pretender que uno deba pagar para enterarse.
Va para largo este tema, así que voy a postear otras cosas entre medio. A la entrevista llegué gracias a pseudopodo
-Bueno, ahora que habla de comerse a los curas, ¿qué le parece la cruzada de Dawkins y Dennet contra Dios?
-Bueno, me parece muy bien. Empezó en el siglo XVIII. Lo malo es que ninguno de esos dos propone ciencia auténtica. Toda la genética que usa Dawkins la inventó él. No existe, nada más que en su imaginación.
Mientras lo apuñalaba, iba subrayando que Dawkins era un gran escritor. Cada vez más adentro. Luego añadió.
-Dawkins y Dennet son los dos únicos filósofos millonarios.
¿Quién es Bunge? Mirando en barrapunto, parece que después de estas declaraciones muchos se olvidaron. Pronto lo van a acusar de no ser ateo, de promover la pseudociencia, de
¿Qué tiene que ver Sagan con esto? Sagan inició esta forma de divulgación científica panfletaria, presentando sus opiniones como científicas. Y encima vendiéndolas, que cada uno tiene derecho a opinar, desde ya, pero no a pretender que uno deba pagar para enterarse.
Va para largo este tema, así que voy a postear otras cosas entre medio. A la entrevista llegué gracias a pseudopodo
23.11.06
1215.- Komarov y Gagarin
Gagarín fue el 1er hombre en el espacio (el sputnik y todo eso), y murió joven, apenas 34 años, después de períodos de alcoholimo, en un accidente de aviación. Komarov fue el 1er hombre que muere en el espacio (en el reingreso de la nave), también murió joven.
Claro, uno puede joder y decir que a Komarov le enseñaron a ponerse en órbita pero no a volver:
o que Gagarin no entendía muy bien el concepto de límite:

o que estaba más preocupado por el recorrido de las bebidas en su estómago:
Pero no es mi intención burlarme de estos capos, todo lo contrario. Me resultan admirables, y me alegro de encontrar escaneados y subidos a la red sus Cuadernos, de Gagarin y de Komarov. También hay una carta de algunos astronautas rusos a Brezhnev, analizando la decadencia del programa ruso (en 1965), señalando el incremento de los vuelos no tripulados y el crecimiento del sector misilístico como causas (postura que los yankis imitarían unos años después, con el apoyo de gente como Sagan).
Nada, eso.
Claro, uno puede joder y decir que a Komarov le enseñaron a ponerse en órbita pero no a volver:

o que Gagarin no entendía muy bien el concepto de límite:

o que estaba más preocupado por el recorrido de las bebidas en su estómago:

Pero no es mi intención burlarme de estos capos, todo lo contrario. Me resultan admirables, y me alegro de encontrar escaneados y subidos a la red sus Cuadernos, de Gagarin y de Komarov. También hay una carta de algunos astronautas rusos a Brezhnev, analizando la decadencia del programa ruso (en 1965), señalando el incremento de los vuelos no tripulados y el crecimiento del sector misilístico como causas (postura que los yankis imitarían unos años después, con el apoyo de gente como Sagan).
Nada, eso.
22.11.06
1214.- Pitagoras y Pell
Ya nos convecimos -creo- que no hay solución con números x e y enteros de la ecuación x2 - 2y2=0.
¿Y de x2 - 2y2=1? ¿o igualando a -1?
Resulta que esta fue más fácil de resolver. Por ejemplo, con x=1, y=1 se tiene una solución igualando a -1. Con x=3, y=2 hay una igualando a 1. Ahora x=7, y=5 cumplen 49-2.25=-1
Así, la recursión
xn+1=xn+2yn
yn+1=xn+yn
nos da soluciones para esta ecuación que es un caso particular de la ecuación de Pell (la general es x2 - Dy2=+-1). Matías redescubrió la recursión en este post, pensándolas como aproximaciones de raíz de 2.
Efectivamente, los pitagóricos llamaron a estos números xn, yn
números diagonal y lado [mi traducción es mala: así como llamaban números triangulares y no triángulos, pentagonales y no pentágonos, etc., deberían ser 'diagonaleales' y 'ladeales', ...verdat? {pronúnciase el '...verdat' como Marianitus Grondoneáea}]
Ahora, como xn, yn crecen 'sin cota' (eufesmismo por 'se van al carajo', el tema es que a los griegos no les gustaba mucho el infinito), si uno divide toda la ecuación de Pell por yn2, el +-1 de la derecha se convierte en una cagadésima despreciable, y se obtiene
xn2 / yn2 -2 = cagadésima despreciable
Es decir, los cocientes de xn, yn aproximan raíz de dos.
(Para interesados, este artículo, Pythagorean side and diagonal numbers de László Filep en el Acta Math. Acad. Paed. Nyíregyháziensis 15 (1999) da una versión más seria y detallada del tema, hay versión pedeéfica)
¿Y de x2 - 2y2=1? ¿o igualando a -1?
Resulta que esta fue más fácil de resolver. Por ejemplo, con x=1, y=1 se tiene una solución igualando a -1. Con x=3, y=2 hay una igualando a 1. Ahora x=7, y=5 cumplen 49-2.25=-1
Así, la recursión
xn+1=xn+2yn
yn+1=xn+yn
nos da soluciones para esta ecuación que es un caso particular de la ecuación de Pell (la general es x2 - Dy2=+-1). Matías redescubrió la recursión en este post, pensándolas como aproximaciones de raíz de 2.
Efectivamente, los pitagóricos llamaron a estos números xn, yn
números diagonal y lado [mi traducción es mala: así como llamaban números triangulares y no triángulos, pentagonales y no pentágonos, etc., deberían ser 'diagonaleales' y 'ladeales', ...verdat? {pronúnciase el '...verdat' como Marianitus Grondoneáea}]
Ahora, como xn, yn crecen 'sin cota' (eufesmismo por 'se van al carajo', el tema es que a los griegos no les gustaba mucho el infinito), si uno divide toda la ecuación de Pell por yn2, el +-1 de la derecha se convierte en una cagadésima despreciable, y se obtiene
xn2 / yn2 -2 = cagadésima despreciable
Es decir, los cocientes de xn, yn aproximan raíz de dos.
(Para interesados, este artículo, Pythagorean side and diagonal numbers de László Filep en el Acta Math. Acad. Paed. Nyíregyháziensis 15 (1999) da una versión más seria y detallada del tema, hay versión pedeéfica)
21.11.06
1213.- Predicciones
Vía Hernán, caigo en esta página de chistes científicos y encuentro el siguiente:
Bueno, no. En los ochenta se siguió reduciendo (este paper es de los ochenta). En realidad, Plutón desapareció en agosto de este año.
Cada vez que se ha hecho algun descubrimiento sobre Pluton ha servido para cambiar las estimaciones de su tamaño - y siempre ha disminuido. De hecho, si en los 60 se hubiese hecho una gráfica del tamaño de Pluton contra el tiempo, mostraría claramente que de seguir esa tendencia el planeta iba a desaparecer en los 80.
Bueno, no. En los ochenta se siguió reduciendo (este paper es de los ochenta). En realidad, Plutón desapareció en agosto de este año.
16.11.06
1212.- Ok, ok, es la ultima
La imagen es del Conway-Guy, y confieso que al principio me despistó:
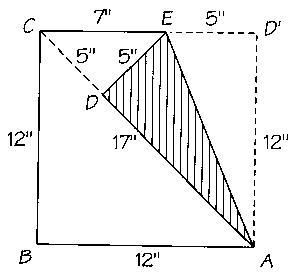
Claro, el 12 y el 17 no tienen nada que ver, la idea es que si raíz de 2 es una fracción a/b, dilatando en b el cuadrado, uno obtendría un cuadrado de lados b, y a es la hipotenusa. Acá no vamos a usar que 2b2=a2, simplemente que con el plegado conseguimos un nuevo cuadradito de lados b-a, es decir, hallamos una fracción con denominador más chico que b. Como el argumento se puede seguir repitiendo, encontramos infinitas fracciones de denominadores cada vez más chicos (y positivos), lo cual no es cierto porque entre 0 y b hay finitos números.

Claro, el 12 y el 17 no tienen nada que ver, la idea es que si raíz de 2 es una fracción a/b, dilatando en b el cuadrado, uno obtendría un cuadrado de lados b, y a es la hipotenusa. Acá no vamos a usar que 2b2=a2, simplemente que con el plegado conseguimos un nuevo cuadradito de lados b-a, es decir, hallamos una fracción con denominador más chico que b. Como el argumento se puede seguir repitiendo, encontramos infinitas fracciones de denominadores cada vez más chicos (y positivos), lo cual no es cierto porque entre 0 y b hay finitos números.
15.11.06
1211.- Analysis by its history
Acabo de terminar el libro de Hairer y Wanner (este). Excelente. Lo leí de un tirón, y en cada hoja encontraba algo nuevo. Me voy a tomar una semanita y lo leo de nuevo. Y con el tiempo, iré posteando algunas de las cosas que encontré.
Por lo pronto, una que nunca había visto en un libro de matemáticas: estereogramas para ilustrar la parte de cálculo en varias variables, dando una impresión de profundidad o 3D.
Por lo pronto, una que nunca había visto en un libro de matemáticas: estereogramas para ilustrar la parte de cálculo en varias variables, dando una impresión de profundidad o 3D.
13.11.06
1210.- Paenza again
El nuevo libro de Adrián Paenza, Matemática estás ahí, episodio 2 está en la calle y también está en la red.
Otra vez, del Depto de Matemáticas de la UBA se puede bajar la versión en pdf, y como la otra vez, les dejo el link para bajarlo: click.
Ahora hay 'menos matemática' y más juegos y problemas de ingenio (je, como si fuesen cosas muy distintas). Mucho material ya circuló por mail, weblogs y demás vía las notas de Página 12. Sospecho que no va a jugarle en contra a las ventas, todo lo contrario. Qué quieren que les diga, más de uno debería seguir el ejemplo de Paenza. Poner el libro gratis en la web no evitó que se convirtiera en un best seller, me animo a decir que todo lo contrario, lo potenció.
Otra vez, del Depto de Matemáticas de la UBA se puede bajar la versión en pdf, y como la otra vez, les dejo el link para bajarlo: click.
Ahora hay 'menos matemática' y más juegos y problemas de ingenio (je, como si fuesen cosas muy distintas). Mucho material ya circuló por mail, weblogs y demás vía las notas de Página 12. Sospecho que no va a jugarle en contra a las ventas, todo lo contrario. Qué quieren que les diga, más de uno debería seguir el ejemplo de Paenza. Poner el libro gratis en la web no evitó que se convirtiera en un best seller, me animo a decir que todo lo contrario, lo potenció.
1209.- Quadratwurzelschnecke
Preguntaba en el post 1199 por la historia de Teodoro mencionada en el Teeteto por Platón, que habría demostrado la irracionalidad de ciertos números hasta el 15, y que no lo hizo para el 17. Hasta el momento, hay varias respuestas:
1.- Platón estaba empédocles cuando escribió lo que escribió, si es que lo escribió, la historia es poco creíble, siempre y cuando haya sido bien traducida, y que no sea una modificación posterior de algún traductor o comentador [hay que reconocer que algunas variantes parece haber: estudió todos los números menores a 17? sólo los impares?]. En la línea de los que dudan están Zeuthen y Heath, conocidos historiadores.
2.- Vía congruencias. Martín comenta en el post anterior que llegó hasta el 13 escribiendo n=13q+r. (aunque el tema sea irracionalidad, y no primalidad, este tipo de argumentos me recuerdan el polinomio de Euler, n2+n+41)
3.- En Gaussianos (link al blog a la derecha, junto con los buenos blogs matemáticos), fede esboza la solución de McCabe (Math Magazine 49-4 de 1976, también en la 5ta edición del Hardy - Wright de teoría de números, pag. 42ss.) La idea es mirar los restos al dividir por 2.
4.- La espiral de Teodoro: no hay que despreciar la posibilidad de que Teodoro parara en el 17 porque no lo necesitaba... resulta que una de sus cosas que sí nos llegó es la siguiente espiral:
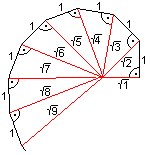
Cada triángulo tiene un ángulo recto, los catetos miden 1 y raíz de n, y la hipotenusa mide raíz de n+1. ¿Qué tiene de interesante aquí el 17? Para 16, se llega a 351 grados y pico, mientras que con 17 se pasa a la vuelta siguiente. ¿Habrá calculado hasta ahí porque era lo que le interesaba para su espiral, y no porque no fuese capaz de demostrarlo para 17?
Vaya uno a saber...
1.- Platón estaba empédocles cuando escribió lo que escribió, si es que lo escribió, la historia es poco creíble, siempre y cuando haya sido bien traducida, y que no sea una modificación posterior de algún traductor o comentador [hay que reconocer que algunas variantes parece haber: estudió todos los números menores a 17? sólo los impares?]. En la línea de los que dudan están Zeuthen y Heath, conocidos historiadores.
2.- Vía congruencias. Martín comenta en el post anterior que llegó hasta el 13 escribiendo n=13q+r. (aunque el tema sea irracionalidad, y no primalidad, este tipo de argumentos me recuerdan el polinomio de Euler, n2+n+41)
3.- En Gaussianos (link al blog a la derecha, junto con los buenos blogs matemáticos), fede esboza la solución de McCabe (Math Magazine 49-4 de 1976, también en la 5ta edición del Hardy - Wright de teoría de números, pag. 42ss.) La idea es mirar los restos al dividir por 2.
4.- La espiral de Teodoro: no hay que despreciar la posibilidad de que Teodoro parara en el 17 porque no lo necesitaba... resulta que una de sus cosas que sí nos llegó es la siguiente espiral:

Cada triángulo tiene un ángulo recto, los catetos miden 1 y raíz de n, y la hipotenusa mide raíz de n+1. ¿Qué tiene de interesante aquí el 17? Para 16, se llega a 351 grados y pico, mientras que con 17 se pasa a la vuelta siguiente. ¿Habrá calculado hasta ahí porque era lo que le interesaba para su espiral, y no porque no fuese capaz de demostrarlo para 17?
Vaya uno a saber...
9.11.06
1208.- Problem(it)a
Dos matemáticos están mirando un polinomio en un pizarrón,
f(x) = anxn +...+ a1x + a0
donde no conocen los coeficientes ak, que son números enteros, ni el grado n.
-A ver, supongamos que la edad de mi hijo es una raíz.
-¿Era 7...?
-No, es más grande. Digamos que f(7)=77.
-A ver, probemos con un número más grande, la edad de mi hija..., ¿qué tal si ahí da 85? ¿Tu mi hijo es más grande que mi hija, no?
-Si, y ahora con esos datos cualquiera puede saber qué edades tienen.
-Listo, preguntemos eso en el parcial, en vez del grado, los coeficientes, y esas boludeces de siempre.
Este problema tiene como 50 años, y no doy la fuente porque no la conozco. En internet aparece en una lista de historia de la matemática en el '97, y en 2000 alguien lo usa en un artículo de educación matemática sin citar nada.
donde no conocen los coeficientes ak, que son números enteros, ni el grado n.
-A ver, supongamos que la edad de mi hijo es una raíz.
-¿Era 7...?
-No, es más grande. Digamos que f(7)=77.
-A ver, probemos con un número más grande, la edad de mi hija..., ¿qué tal si ahí da 85? ¿Tu mi hijo es más grande que mi hija, no?
-Si, y ahora con esos datos cualquiera puede saber qué edades tienen.
-Listo, preguntemos eso en el parcial, en vez del grado, los coeficientes, y esas boludeces de siempre.
Este problema tiene como 50 años, y no doy la fuente porque no la conozco. En internet aparece en una lista de historia de la matemática en el '97, y en 2000 alguien lo usa en un artículo de educación matemática sin citar nada.
8.11.06
1207.- Ahora de numeros otra vez
Si, ya nos convencimos de que raíz de dos es irracional, pero ahí va otra: si es a/b,
a2=2b2
y del lado izquierdo hay un número par de divisores, mientras que en el derecho son impares.
Upgrade 1207.1: me señala Hernán -con mucha razón- que en vez de divisores debería decir factores primos.
y del lado izquierdo hay un número par de divisores, mientras que en el derecho son impares.
Upgrade 1207.1: me señala Hernán -con mucha razón- que en vez de divisores debería decir factores primos.
7.11.06
1206.- Otra clase de irracionalidad
(Nada que ver con todo lo anterior) Esto es por el artículo de Eleanor Robson, Iraq: the history of mathematics and the aftermath of war, British Society for the History of Mathematics Newsletter 49 (2003), 1-9.
Otra historia similar: un tanque voló el frente de la Academia de Ciencias de Irak, para sacar la bandera... tras eso, el 80 por ciento de los 58000 libros y los 2000 manuscritos que había fueron robados.
The Awqaf, established in 1920, held some 7,000 manuscripts, mostly religious, but also including important early scientific works. Staff managed to move most of the collection to safety before the war, sending about a quarter of it, mostly comprising recently acquired material, under armed guard to a mosque. But when one of those guards was shot and killed by US troops on 14 April and the others disarmed, it was decided that the collection would be safer in the Awqaf building after all. That afternoon the library was set upon by organised looters, who stole 22 of the 32 trunks containing the returned manuscripts and then set fire to the building with flammable agents. The whole structure burned to the ground within quarter of an hour; an estimated 700 manuscripts were destroyed in the blaze and a further thousand or so looted.
Otra historia similar: un tanque voló el frente de la Academia de Ciencias de Irak, para sacar la bandera... tras eso, el 80 por ciento de los 58000 libros y los 2000 manuscritos que había fueron robados.
6.11.06
1205.- Logicas ilogicas
Venía dando vueltas sobre el tema de la irracionalidad porque muchas veces algo se califica de irracional pero sin especificar en relación a qué.
En aritmética, irracional no apunta a un número que escapa de la razón (un número inexplicable, o absurdo, o imposible, o que no entra en la cabeza...), sino a uno que no puede representarse como un cociente -o razón- de cantidades enteras.
De la misma manera, que un pensamiento, deducción, creencia, etc. sea irracional está asociado en nuestra cultura a la lógica aristotélica. Tenemos tan arraigado esto que hasta hace unos cien años nadie se cuestionó que podía haber diferentes lógicas, y si esto ocurrió, fue más por culpa de Cantor y su introducción de los distintos infinitos que por otra cosa.
Se quejaba en un comment Osvaldo que por cambiar algún postulado de la lógica clásica no es cuestión de llamar irracional a estas nuevas lógicas, lógicas ilógicas en el sentido tradicional, pero matemáticamente interesantes.
Uno de los intentos más interesantes acepta cierto grado de inconsistencia, para lo cual se deja de lado el principio del 3ro excluído y el ex contradictione quodlibet (de una contradicción se deduce cualquier cosa).
Para mas info al respecto, Inconsistent mathematics, en la Enciclopedia de Filosofía de Stanford. Su autor, Chris Mortensen, escribió un libro sobre el tema que comenta Baez aquí. También, un par de link con laburos actuales en el tema: WoPalo, y artículos; y la entrada de la Wikipedia sobre lógicas paraconsistentes.
En aritmética, irracional no apunta a un número que escapa de la razón (un número inexplicable, o absurdo, o imposible, o que no entra en la cabeza...), sino a uno que no puede representarse como un cociente -o razón- de cantidades enteras.
De la misma manera, que un pensamiento, deducción, creencia, etc. sea irracional está asociado en nuestra cultura a la lógica aristotélica. Tenemos tan arraigado esto que hasta hace unos cien años nadie se cuestionó que podía haber diferentes lógicas, y si esto ocurrió, fue más por culpa de Cantor y su introducción de los distintos infinitos que por otra cosa.
Se quejaba en un comment Osvaldo que por cambiar algún postulado de la lógica clásica no es cuestión de llamar irracional a estas nuevas lógicas, lógicas ilógicas en el sentido tradicional, pero matemáticamente interesantes.
Uno de los intentos más interesantes acepta cierto grado de inconsistencia, para lo cual se deja de lado el principio del 3ro excluído y el ex contradictione quodlibet (de una contradicción se deduce cualquier cosa).
Para mas info al respecto, Inconsistent mathematics, en la Enciclopedia de Filosofía de Stanford. Su autor, Chris Mortensen, escribió un libro sobre el tema que comenta Baez aquí. También, un par de link con laburos actuales en el tema: WoPalo, y artículos; y la entrada de la Wikipedia sobre lógicas paraconsistentes.
3.11.06
1204.- El paper Nature de la semana
Se merece el lugar destacado el paper sobre "The DNA sequence and biological annotation of human chromosome 1".
Pero ojo, no el paper "The DNA sequence and biological annotation of human chromosome 1", que se publicó en mayo, sino el que se publicó el jueves 26 de octubre:
"Corregidendum: The DNA sequence and biological annotation of human chromosome 1", Nature 443.
¿En qué le pifiaron? Se olvidaron de incluír 13 coautores... Esperemos que los 3.141 genes, 991 pseudogenes, y las many coding sequences estén todas bien anotaditas y no se hayan olvidado de incluír nada.
(vía improbable research)
Pero ojo, no el paper "The DNA sequence and biological annotation of human chromosome 1", que se publicó en mayo, sino el que se publicó el jueves 26 de octubre:
"Corregidendum: The DNA sequence and biological annotation of human chromosome 1", Nature 443.
¿En qué le pifiaron? Se olvidaron de incluír 13 coautores... Esperemos que los 3.141 genes, 991 pseudogenes, y las many coding sequences estén todas bien anotaditas y no se hayan olvidado de incluír nada.
(vía improbable research)
1203.- Deducciones irracionales
Escribiendo el post anterior, caigo en la cuenta que Baez (éste) le está contestando (conscientemente o no) a los Sokal-istas cuando defienden:
(Sokal aclara en su paper que vive en un piso 22).
Estaremos de acuerdo que la ciencia no es una mera convención social, pero aún creyendo eso, nadie saca a partir de allí deducciones tan absurdas como para que se contradigan abiertamente con la realidad. Hay un límite en la realidad para la aplicabilidad de la tablita de verdad.
Y un tema aparte es la cantidad de factores a considerar en un problema de corte menos exacto, como para poder distinguir claramente cuál es la hipótesis errónea que lleva a un absurdo. Estoy seguro que diferentes hipótesis, todas razonables consideradas por separado, pueden llevar a conclusiones absurdas interactuando todas juntas... me parece que el campo de la economía es el lugar correcto para buscar ejemplos.
Upgrade 1203.1: siguiendo el consejo de dotuev, aclaremos que la cosa no es con Sokal, sino con sus seguidores, que muchas veces son más papistas que el Papa.
los que crean que la ciencia es una mera convención social, prueben transgredirla tirándose por mi ventana
(Sokal aclara en su paper que vive en un piso 22).
Estaremos de acuerdo que la ciencia no es una mera convención social, pero aún creyendo eso, nadie saca a partir de allí deducciones tan absurdas como para que se contradigan abiertamente con la realidad. Hay un límite en la realidad para la aplicabilidad de la tablita de verdad.
Y un tema aparte es la cantidad de factores a considerar en un problema de corte menos exacto, como para poder distinguir claramente cuál es la hipótesis errónea que lleva a un absurdo. Estoy seguro que diferentes hipótesis, todas razonables consideradas por separado, pueden llevar a conclusiones absurdas interactuando todas juntas... me parece que el campo de la economía es el lugar correcto para buscar ejemplos.
Upgrade 1203.1: siguiendo el consejo de dotuev, aclaremos que la cosa no es con Sokal, sino con sus seguidores, que muchas veces son más papistas que el Papa.
2.11.06
1202.- Mas irracionalidades (pero no de numeros)
Una de esas leyes lógicas que todos sabemos es la de que un resultado falso implica cualquier cosa. En realidad, es una línea en la tabla de verdad de las implicaciones, si p es falso y p implica q, p implica q es verdadero aunque q sea cualquier banana.
Circula una anécdota -que Smullyan atribuye a Russell, otros a Hardy- según la cual alguien -a veces un filósofo, otras gente común, nunca uno de ciencias- se muestra escéptico al respecto -che! que el escepticismo tiene un límite... con ciertas cosas no se jode- y le pide que demuestre que si 1=2, Russell y el Papa son la misma persona. Como él y el Papa son dos personas, pero ya que él es uno, y uno es igual a dos, él es el Papa, argumenta Russell, y el otro se cae'e culo y ve la Luz1. Igual, esta parte no suele estar muy detallada en la anécdota, pero parece que lo convence porque si el otro hubiese dado una réplica interesante, figuraría.
Una réplica interesante la dió Baez varias décadas después: si en una cadena de razonamientos uno llega a un resultado falso o que contradice lo que creemos, lo normal es que uno no salte por la ventana porque eso implica que uno puede volar.
Y los matemáticos lo sabemos bien: cuando llegamos a una contradicción, uno se frena, y en lugar de declarar que vale todo, retrocede buscando dónde estuvo la falla (algún error humano en la deducción) o qué suposición que uno hizo es demasiado atrevida para descartarla (apelando al ppio. del 3ro excluído)2.
Pero todo eso parte de una suposición previa, y es que la premisa es verdadera ó falsa. La cosa se complica cuando uno rechaza esto y entra en las lógicas multivaluadas, donde una proposición A puede ser:
-verdadera, falsa, o indecidible.
-verdadera (1), falsa (0), ó p, con p entre 0 y 1 (fuzzy, probabilidades).
-1, 0, ó n valores extras (Lucasiewicz y Tarski)
Pero todo se pone realmente irracional si uno acepta:
-verdadera, falsa, ó ambas.
(Continuará... O no, o ambas cosas)
(1) es lógico que si queda de espaldas en el suelo vea la Luz, porque esta suele venir de arriba, ya sea el sol, un foco, etc.
(2) ya habíamos hablado del ppio. del 3ro excluído con la excusa de las demostraciones por el absurdo acá, acá y acá
Circula una anécdota -que Smullyan atribuye a Russell, otros a Hardy- según la cual alguien -a veces un filósofo, otras gente común, nunca uno de ciencias- se muestra escéptico al respecto -che! que el escepticismo tiene un límite... con ciertas cosas no se jode- y le pide que demuestre que si 1=2, Russell y el Papa son la misma persona. Como él y el Papa son dos personas, pero ya que él es uno, y uno es igual a dos, él es el Papa, argumenta Russell, y el otro se cae'e culo y ve la Luz1. Igual, esta parte no suele estar muy detallada en la anécdota, pero parece que lo convence porque si el otro hubiese dado una réplica interesante, figuraría.
Una réplica interesante la dió Baez varias décadas después: si en una cadena de razonamientos uno llega a un resultado falso o que contradice lo que creemos, lo normal es que uno no salte por la ventana porque eso implica que uno puede volar.
Y los matemáticos lo sabemos bien: cuando llegamos a una contradicción, uno se frena, y en lugar de declarar que vale todo, retrocede buscando dónde estuvo la falla (algún error humano en la deducción) o qué suposición que uno hizo es demasiado atrevida para descartarla (apelando al ppio. del 3ro excluído)2.
Pero todo eso parte de una suposición previa, y es que la premisa es verdadera ó falsa. La cosa se complica cuando uno rechaza esto y entra en las lógicas multivaluadas, donde una proposición A puede ser:
-verdadera, falsa, o indecidible.
-verdadera (1), falsa (0), ó p, con p entre 0 y 1 (fuzzy, probabilidades).
-1, 0, ó n valores extras (Lucasiewicz y Tarski)
Pero todo se pone realmente irracional si uno acepta:
-verdadera, falsa, ó ambas.
(Continuará... O no, o ambas cosas)
(1) es lógico que si queda de espaldas en el suelo vea la Luz, porque esta suele venir de arriba, ya sea el sol, un foco, etc.
(2) ya habíamos hablado del ppio. del 3ro excluído con la excusa de las demostraciones por el absurdo acá, acá y acá
1.11.06
1201.- Irracionales (II)
Y antes de meterme con cosas realmente irracionales, otra demostración sencilla y fácil de recordar, que utiliza sólo la definición de logaritmo: log2(3) es irracional. Veamos:
Si log2(3)=a/b con a, b enteros,
2(a/b)=3, o sea
2a=3b,
lo cual no puede ser porque un lado es múltiplo exclusivamente de 2 y el otro de 3.
No es difícil demostrar en la misma línea que si m no es una potencia de n, entonces logn(m) no puede ser racional.
Y sobre la irracionalidad en general, pero en otro tema, les recomiendo este excelente post de Alejandro. Pensaba dejarle un comment, pero mejor lo incluyo acá: can I ask if mathematics is 'rational'? (that is, self-consistent or non-contradictory)
lo cual no puede ser porque un lado es múltiplo exclusivamente de 2 y el otro de 3.
No es difícil demostrar en la misma línea que si m no es una potencia de n, entonces logn(m) no puede ser racional.
Y sobre la irracionalidad en general, pero en otro tema, les recomiendo este excelente post de Alejandro. Pensaba dejarle un comment, pero mejor lo incluyo acá: can I ask if mathematics is 'rational'? (that is, self-consistent or non-contradictory)
31.10.06
1200.- Convencimiento: posts osados o plomos
Post mío: vasos densos (mosto convencional, dos pesos) + conocimiento: post plomo.
Polvo tonto, ósmosis, lo vomito, descompensacion... Descompensación: post sonso.
Polvo tonto, ósmosis, lo vomito, descompensacion... Descompensación: post sonso.
30.10.06
1199.- Irracionales
Hay cosas irracionales sobre los números irracionales.
Se comenta por ahí que un griego de hace dos milenios y medio demostró que las raíces cuadradas de 2, 3, 5, 7, 8, 10, 11, 12, 13, 14 y 15 no eran racionales, pero que no pudo demostrarlo para el 17.
No se me ocurre qué clase de argumento habrá usado. ¿Congruencias, tal vez?
Para no ser incongruente, aclaro qué quiero decir con eso: por ejemplo, si elevamos un número al cuadrado hay sólo dos opciones, es divisible por 3 ó es de la forma 3k+1, es decir, al dividirlo tiene resto 1. Ahora, si raíz de 2 fuera a/b, donde a y b no tienen factores comunes,
a2=2b2
con lo cual el lado izquierdo y el derecho no pueden tener el mismo resto si los dividimos por 3.
Esta demostración es de Enzo Gentile, más conocido por sus Notas de álgebra o su tango El Algebrista.
Se comenta por ahí que un griego de hace dos milenios y medio demostró que las raíces cuadradas de 2, 3, 5, 7, 8, 10, 11, 12, 13, 14 y 15 no eran racionales, pero que no pudo demostrarlo para el 17.
No se me ocurre qué clase de argumento habrá usado. ¿Congruencias, tal vez?
Para no ser incongruente, aclaro qué quiero decir con eso: por ejemplo, si elevamos un número al cuadrado hay sólo dos opciones, es divisible por 3 ó es de la forma 3k+1, es decir, al dividirlo tiene resto 1. Ahora, si raíz de 2 fuera a/b, donde a y b no tienen factores comunes,
con lo cual el lado izquierdo y el derecho no pueden tener el mismo resto si los dividimos por 3.
Esta demostración es de Enzo Gentile, más conocido por sus Notas de álgebra o su tango El Algebrista.
29.10.06
26.10.06
1196.- GOTO
la computadora es como la vida misma. los programas nacen, crecen, escriben y leen algunas cosas, con suerte se reproducen y mueren. y asi n veces, un programa cree ser único en su clase, pero no sabe que en la dirección de memoria 0xA2000 quizás haya un clon de él, creyendo que es el único tambien.
el kernel del sistema operativo vendría a ser como el programa que ejecuta a nuestro universo. estuvo ahi miles de milisegundos antes que nosotros, y presenciará el reset final de todo. lo malo es que nunca podrá hacer un dump de memoria.
y el kernel, como el universo, rearrancará miles de veces creyendo no sólo ser único sino estar viviendo un tiempo irrepetible.
cuando en realidad, todo lo que hace es seguir instrucciones tan claramente pautadas que de obvias son invisibles.
este no cambia. Lo único lamentable es que se hayan perdido sus muchos posts como argentino standard. Como escribió alguna vez: si fuera el arquero de la selección natural, todavía seríamos unicelulares.
23.10.06
1195.- Ptolomeo
Pocos científicos han sido más despreciados que Ptolomeo (tal vez, Aristóteles) y su obra no llega a hacerse conocida por la 'superioridad' del modelo copernicano. Recordemos brevemente que el ptolemaico fue el primer modelo matemático que permitió calcular la posición de los planetas y el sol, un modelo lo suficientemente preciso como para calcularlas durante unos quince siglos.
Claro: el modelo copernicano es mejor, me dirán, el sol está en el centro, y los planetas se mueven en círculos a su alrededor... Momento! que los planetas no se mueven en círculos en torno al sol, se mueven en elipses, y eso lo propuso Kepler. Y tampoco: las perturbaciones en las órbitas elípticas se observaron hace mucho tiempo. La teoría de Newton indicaba cómo hacer los cálculos astronómicos, pero si hasta el siglo XIX se pensó que era suficiente considerar el tironeo gravitatorio entre los planetas para explicarlas, con Poincaré se llegó a la conclusión de que ese camino no funcionaba. Con la relatividad en el siglo XX se introdujeron más factores a considerar: velocidades, masas, etc., pero el cálculo no mejoró hasta la aparición de la computadora. Y ahí no hubo ninguna revolución conceptual (o tal vez sí, pero fue un retroceso: creer que los números que la máquina escupen son verdaderos).
¿Y qué se hizo con la máquina? Simplemente, integrar numéricamente las ecuaciones que no se podían integrar en forma 'cerrada' como combinación finita de las funciones conocidas, una versión muy sofisticada de los métodos de Euler del siglo XVII pero nada más. Pregúntenle al Ariadnne 5 qué pasa con los pequeños errores numéricos aún cuando se quiere ser preciso.
Ahora, siglo XXI, sabemos que la computadora tampoco es la solución al problema: Marsden (el mismo del Marsden Tromba que se usa en Análisis II) demostró hace unos pocos años que no existen métodos numéricos simplécticos: las trayectorias numéricas pueden calcular bastante bien la posición, pero no las cantidades conservadas (como momentos, o la energía), lo cual a la larga influye negativamente en el cálculo de la posición. El resultado es tan negativo que el viejo péndulo determinístico de Huyghens se vuelve caótico, y si tenemos en cuenta que una masa rotando circularmente -sea el sol en torno a la tierra o al revés- es el péndulo más simple de describir, vemos cómo afecta al problema.
¿Y dónde quedará el cálculo de las órbitas en el futuro? ¿Se reirá alguien -mañana- de esta gente como algunos se ríen hoy de Ptolomeo? Sospecho que sí, lamentablemente.
Claro: el modelo copernicano es mejor, me dirán, el sol está en el centro, y los planetas se mueven en círculos a su alrededor... Momento! que los planetas no se mueven en círculos en torno al sol, se mueven en elipses, y eso lo propuso Kepler. Y tampoco: las perturbaciones en las órbitas elípticas se observaron hace mucho tiempo. La teoría de Newton indicaba cómo hacer los cálculos astronómicos, pero si hasta el siglo XIX se pensó que era suficiente considerar el tironeo gravitatorio entre los planetas para explicarlas, con Poincaré se llegó a la conclusión de que ese camino no funcionaba. Con la relatividad en el siglo XX se introdujeron más factores a considerar: velocidades, masas, etc., pero el cálculo no mejoró hasta la aparición de la computadora. Y ahí no hubo ninguna revolución conceptual (o tal vez sí, pero fue un retroceso: creer que los números que la máquina escupen son verdaderos).
¿Y qué se hizo con la máquina? Simplemente, integrar numéricamente las ecuaciones que no se podían integrar en forma 'cerrada' como combinación finita de las funciones conocidas, una versión muy sofisticada de los métodos de Euler del siglo XVII pero nada más. Pregúntenle al Ariadnne 5 qué pasa con los pequeños errores numéricos aún cuando se quiere ser preciso.
Ahora, siglo XXI, sabemos que la computadora tampoco es la solución al problema: Marsden (el mismo del Marsden Tromba que se usa en Análisis II) demostró hace unos pocos años que no existen métodos numéricos simplécticos: las trayectorias numéricas pueden calcular bastante bien la posición, pero no las cantidades conservadas (como momentos, o la energía), lo cual a la larga influye negativamente en el cálculo de la posición. El resultado es tan negativo que el viejo péndulo determinístico de Huyghens se vuelve caótico, y si tenemos en cuenta que una masa rotando circularmente -sea el sol en torno a la tierra o al revés- es el péndulo más simple de describir, vemos cómo afecta al problema.
¿Y dónde quedará el cálculo de las órbitas en el futuro? ¿Se reirá alguien -mañana- de esta gente como algunos se ríen hoy de Ptolomeo? Sospecho que sí, lamentablemente.
20.10.06
1194.- Hilbert y Poincare
Cien años atrás, los matemáticos más importantes del mundo eran Hilbert y Poincaré. Su influencia nos llega hasta el día de hoy (la lista de 23 problemas de Hilbert guió la investigación de muchísimos matemáticos de primera línea; grandes partes -cuando no la teoría entera- de topología y geometría algebraica, sistemas dinámicos, teoría ergódica, funciones complejas, y geometría diferencial comenzaron con Poincaré).
Sin embargo, son mucho menos conocidos que Einstein, y cosas como éstas nos dicen que no debería ser así.
(Con Poincaré no hubo dudas: publicó sus cosas antes, incluso las mencionó en libros de divulgación, le corrigió un error a Lorentz, y el propio Einstein reconoció que Poincaré lo había hecho antes)
Sin embargo, son mucho menos conocidos que Einstein, y cosas como éstas nos dicen que no debería ser así.
(Con Poincaré no hubo dudas: publicó sus cosas antes, incluso las mencionó en libros de divulgación, le corrigió un error a Lorentz, y el propio Einstein reconoció que Poincaré lo había hecho antes)
17.10.06
1193.- What time is it?
Now.
No voy a arruinarlo comentando. Les recomiendo revisar otros.
Upgrade 1193.1: Si, como yo, venían leyendo desde el primero, empiecen de vuelta leyendo la frase que aparece cuando dejan quieto el mouse sobre la imagen.
No voy a arruinarlo comentando. Les recomiendo revisar otros.
Upgrade 1193.1: Si, como yo, venían leyendo desde el primero, empiecen de vuelta leyendo la frase que aparece cuando dejan quieto el mouse sobre la imagen.
13.10.06
1192.- Topalov - Kramnik
Ayer se cortó blogger y no pude postear más. Y hoy se cortó la transmisión del desempate... Como sea, ya hay campeón: Vladimir ("memeo-o-melameneo") Kramnik. Si no hubiese ganado él, hoy habría un nuevo juicio, porque jugó bajo protesta sin aceptar el punto perdido en la rueda que no se presentó.
Bien o mal, se resolvió una situación que llevaba más de diez años: un título 'clásico' en manos de Kramnik que se lo ganó a Kasparov, un título 'oficial' que entregaba la fide año a año en un torneo masivo donde se eliminaban los participantes en enfrentamientos mano a mano, y un título 'de hecho', en manos de Kasparov, que le ganaba a cualquiera en cualquier lado. Y su retiro del tablero era necesario para esta reunificación.
Bue, ya está... habrá que volver a las matemáticas hasta dentro de dos meses, cuando Kramnik se enfrente a Fritz 9 en otro human-computer match.
Upgrade 1192.1: un detalle: de 16 partidos (o quince), sólo hubo siete tablas, menos de la mitad de los partidos, y lo que más sorprende, con defensas tan secas como la eslava. Ese, sin dudas, es el poder de la computadora: posiciones evaluadas antes como tablas presentan pequeños desequilibrios que sólo el potente poder de cálculo de los programas modernos pueden descubrir. Líneas teóricas casi descartadas se reconsideran, y la preparación previa es más importante que nunca. Qué seguirá? Vaya uno a saber.
Bien o mal, se resolvió una situación que llevaba más de diez años: un título 'clásico' en manos de Kramnik que se lo ganó a Kasparov, un título 'oficial' que entregaba la fide año a año en un torneo masivo donde se eliminaban los participantes en enfrentamientos mano a mano, y un título 'de hecho', en manos de Kasparov, que le ganaba a cualquiera en cualquier lado. Y su retiro del tablero era necesario para esta reunificación.
Bue, ya está... habrá que volver a las matemáticas hasta dentro de dos meses, cuando Kramnik se enfrente a Fritz 9 en otro human-computer match.
Upgrade 1192.1: un detalle: de 16 partidos (o quince), sólo hubo siete tablas, menos de la mitad de los partidos, y lo que más sorprende, con defensas tan secas como la eslava. Ese, sin dudas, es el poder de la computadora: posiciones evaluadas antes como tablas presentan pequeños desequilibrios que sólo el potente poder de cálculo de los programas modernos pueden descubrir. Líneas teóricas casi descartadas se reconsideran, y la preparación previa es más importante que nunca. Qué seguirá? Vaya uno a saber.
1191.- Lo bueno de tener un blog
...es que si se te rompe la computadora, lectores y amigos te recomiendan links. Claro, al principio no se los puede ver ni postear, pero en unos días sí. Así que acá van algunos:
-parecía que Penny Smith había resuelto uno de los problemas del Clay, las ecuaciones de Navier Stokes. P. Woit lo posteó hace una semana, pero me avisan que en la página de PS apareció una retractación, ya que se detectaron errores en la demostración. De paso, los avances más importantes en este problema se deben a un matemático argentino y me comentan que él cree que que la solución será negativa.
-por otro lado, me recomiendan leer este post, sobre Thurston, Wittgenstein, y qué quiere decir 'entender' en matemáticas. Lo tengo que leer con más cuidado, y revisar un poco la discusión que hay sobre los temas que toca, sobre todo porque soy de los que buscan distintas demostraciones para un mismo resultado.
-me pasan un link a maps of wars, ¿quién controló el medio oriente?
-parecía que Penny Smith había resuelto uno de los problemas del Clay, las ecuaciones de Navier Stokes. P. Woit lo posteó hace una semana, pero me avisan que en la página de PS apareció una retractación, ya que se detectaron errores en la demostración. De paso, los avances más importantes en este problema se deben a un matemático argentino y me comentan que él cree que que la solución será negativa.
-por otro lado, me recomiendan leer este post, sobre Thurston, Wittgenstein, y qué quiere decir 'entender' en matemáticas. Lo tengo que leer con más cuidado, y revisar un poco la discusión que hay sobre los temas que toca, sobre todo porque soy de los que buscan distintas demostraciones para un mismo resultado.
-me pasan un link a maps of wars, ¿quién controló el medio oriente?
12.10.06
1190.- Kramnik - Topalov
Se está jugando el último partido del match, están igualados en puntos y Topalov va con negras. Van por la movida 15 y la posición es equilibrada.
Topalov debería iniciar el ataque por la columna h que está abierta, pero hay que ver cómo contra-atacará Kramnik (o si se defenderá) en el flanco dama, que puede iniciar una especie de ataque de minorías.
Upgrade 1190.1: Topalov eligió defenderse, y no me gusta su posición (al Fritz tampoco). Lo que sigue ahora es técnica standard, el blanco avanza los peones a y b; el negro los 'cambia' por los peones a, b, y c; el blanco queda con peón de más pero en las simplificaciones se puede caer -muy fácil- en una posición tablas o en un final perdido.
Topalov debería iniciar el ataque por la columna h que está abierta, pero hay que ver cómo contra-atacará Kramnik (o si se defenderá) en el flanco dama, que puede iniciar una especie de ataque de minorías.
Upgrade 1190.1: Topalov eligió defenderse, y no me gusta su posición (al Fritz tampoco). Lo que sigue ahora es técnica standard, el blanco avanza los peones a y b; el negro los 'cambia' por los peones a, b, y c; el blanco queda con peón de más pero en las simplificaciones se puede caer -muy fácil- en una posición tablas o en un final perdido.
6.10.06
5.10.06
1188.- El tablero inodoro no se mancha
Hay cosas que se prestan casi para la joda:
-el 'manager' o algo así de Topalov calculó cuántas de las movidas de Kramnik eran las recomendadas por el Fritz 9, y obtuvo un promedio del 78% (en algunos partidos, del 88%). Desde ya, números aisaldos no dicen nada, a mi me asombró hace unos años cuando revisaba partidos de Alekhine (el 2do libro de sus mejores partidos) cómo coincidía con las recomendaciones del Fritz 4, la diferencia estaba apenas en las movidas de ataque muy profundas y sutiles, en algún sacrificio, etc. Alguien tendría que tomarse el trabajo de ver qué pasa con las de Topalov (a priori, y habiendo analizado bastante con máquinas, me juego a que debe dar parecido).
-El match estaba 2-0 para Kramnik, ahora está 2-2 (una porque Kramnik no se presentó, la otra hoy la ganó Topalov por paliza)
-Los GM apoyan a Kramnik (¿se olvidaron de sus acusaciones contra Topalov por el mismo tema?)
-Kasparov escribe para el Wall Street Journal y les pega a todos por igual, recordando cómo la FIDE protegió en su momento a Karpov contra él.
-El equipo de Kramnik denuncia que alguien del equipo de Topalov podría plantarle algo a Kramnik en el baño o la sala de descanso (¿les faltará algún cablecito?).
-el 'manager' o algo así de Topalov calculó cuántas de las movidas de Kramnik eran las recomendadas por el Fritz 9, y obtuvo un promedio del 78% (en algunos partidos, del 88%). Desde ya, números aisaldos no dicen nada, a mi me asombró hace unos años cuando revisaba partidos de Alekhine (el 2do libro de sus mejores partidos) cómo coincidía con las recomendaciones del Fritz 4, la diferencia estaba apenas en las movidas de ataque muy profundas y sutiles, en algún sacrificio, etc. Alguien tendría que tomarse el trabajo de ver qué pasa con las de Topalov (a priori, y habiendo analizado bastante con máquinas, me juego a que debe dar parecido).
-El match estaba 2-0 para Kramnik, ahora está 2-2 (una porque Kramnik no se presentó, la otra hoy la ganó Topalov por paliza)
-Los GM apoyan a Kramnik (¿se olvidaron de sus acusaciones contra Topalov por el mismo tema?)
-Kasparov escribe para el Wall Street Journal y les pega a todos por igual, recordando cómo la FIDE protegió en su momento a Karpov contra él.
-El equipo de Kramnik denuncia que alguien del equipo de Topalov podría plantarle algo a Kramnik en el baño o la sala de descanso (¿les faltará algún cablecito?).
1.10.06
1187.- El inodoro tablero no se mancha
Veselin Topalov (para mí, el heredero -por ésto y por ésto) y Vladimir Kramnik están reunificando el título mundial de ajedrez. O estaban.
Recapitulemos, que si bien de VT hemos hablado bastante en el blog, de VK no. Recordemos que le ganó un match soporífero a Kasparov, con lo cual se convirtió en el campeón "no oficial", aunque la FIDE luego lo reconoció (todo sea por vender una reunificación...). Topalov venía como el candidato de San Luis (no, ése en el que está pensando no; el candidato de San Luis porque allí ganó el torneo frente a los mejores ajedrecistas). Y habían empezado a jugar en Elista la reunificación.
Pero después del cuarto partido, con el marcador 3-1 a favor de Kramnik...:
15.54 Kramnik plays move 15
15.55 Goes into the bathroom
15.56 Goes out of the bathroom
15.57 Goes into the bathroom
15.59 Goes out of the bathroom
16.03 Goes into the bathroom
16.04 Goes out the bathroom
16.07 Comes out for move 16
A Topalov se le soltó la cadena1 y denuncia que Kramnik fue 50 veces al baño durante el partido y 25 a la sala de descanso (dando a entender que como ahí no hay vigilancia, puede haber recibido asesoramiento) y pide que se prohiba el uso de los baños o que un árbitro acompañe a los jugadores.
Ofendido, Kramnik no se presentó al quinto partido2, y no se sabe qué pasará mañana; el partido de hoy -sexto- se suspendió, y Kramnik exigía que se volviera atrás y se jugara el quinto.
Mas info, Toiletgate y full crisis blog.
(1) Y a K el cuerito...
(2) Fuentes no fidedignas -y la tribuna- dicen "K se garcó"3
(3) De ser así, tal vez se entenderían tantos viajes al ñoba
Upgrade 1187.1: Empezó el 6to partido, el match está 3-2 para Kramnik. Se lo puede ver online acá.
Recapitulemos, que si bien de VT hemos hablado bastante en el blog, de VK no. Recordemos que le ganó un match soporífero a Kasparov, con lo cual se convirtió en el campeón "no oficial", aunque la FIDE luego lo reconoció (todo sea por vender una reunificación...). Topalov venía como el candidato de San Luis (no, ése en el que está pensando no; el candidato de San Luis porque allí ganó el torneo frente a los mejores ajedrecistas). Y habían empezado a jugar en Elista la reunificación.
Pero después del cuarto partido, con el marcador 3-1 a favor de Kramnik...:
15.54 Kramnik plays move 15
15.55 Goes into the bathroom
15.56 Goes out of the bathroom
15.57 Goes into the bathroom
15.59 Goes out of the bathroom
16.03 Goes into the bathroom
16.04 Goes out the bathroom
16.07 Comes out for move 16
A Topalov se le soltó la cadena1 y denuncia que Kramnik fue 50 veces al baño durante el partido y 25 a la sala de descanso (dando a entender que como ahí no hay vigilancia, puede haber recibido asesoramiento) y pide que se prohiba el uso de los baños o que un árbitro acompañe a los jugadores.
Ofendido, Kramnik no se presentó al quinto partido2, y no se sabe qué pasará mañana; el partido de hoy -sexto- se suspendió, y Kramnik exigía que se volviera atrás y se jugara el quinto.
Mas info, Toiletgate y full crisis blog.
(1) Y a K el cuerito...
(2) Fuentes no fidedignas -y la tribuna- dicen "K se garcó"3
(3) De ser así, tal vez se entenderían tantos viajes al ñoba
Upgrade 1187.1: Empezó el 6to partido, el match está 3-2 para Kramnik. Se lo puede ver online acá.
30.9.06
1186.- Historias de la ciencia (que nunca se cuentan)
Tres papers publicados independientemente en 1932 por Zener, Landauy Stueckelberg introdujeron el fenómeno conocido hoy como "Landau-Zener tunneling".
(así empieza este paper)
Para otras historias sobre el pobre Stueckelberg, ver aquí.
27.9.06
25.9.06
1184.- Evolucion
Algún día tendría que hacer un análisis detallado de los personajes involucrados en los grandes avances en la teoría de evolución.
¿Alguien me da una mano con los nombres que no deberían falta?
¿Alguien me da una mano con los nombres que no deberían falta?
21.9.06
1183.- Sigue la novela
A dos meses del ICM posteaba que había aparecido una demostración de dos chinos que completaba los trabajos de Perelman, y me preguntaba (en los comments) si no estaría atrás de todo la mano de Yau para llegar a la fecha del congreso mundial con el estatus de la conjetura resuelto y que se le otorgara la Field a Perelman.
Otros, en cambio, afirmaban que Yau y compañía estaban robando el trabajo de Perelman (Sampedro en El País, Nasar y Gruber en el New Yorker, bloggers varios), y ahora un amigo me avisa que Yau los acusa de difamación. A Nassar, Gruber y el New Yorker, por ahora, pero también hay bloggers que han recibido el link en forma anónima sin otros comentarios (ars mathematica), y efectivamente en el anteúltimo parrafo del escrito que sus abogados enviaron a Nassar y Cía piden que se retracten el diario y menciona los blogs.
Recuerdo que cuando leí el artículo de Nasar y Gruber (me lo envió este mismo amigo) me pareció tan malo que decidí no linkearlo; también intenté una defensa de Yau en un blog español que lo atacó duramente (pero se hicieron los pelotudos y ni me contestaron, espero que no les llegue ahora una demanda a ellos también :P).
Linda novelita se vino... y eso que todavía el Clay no se pronunció sobre el millón de dólares, ni nadie lo reclamó.
Más posts al respecto: acá, cuando se confirmó que Perelman ganaba la Field; motl; woit; kottke; asymptotia; y también blogs no matemáticos como regret the error o infropoc.
Otros, en cambio, afirmaban que Yau y compañía estaban robando el trabajo de Perelman (Sampedro en El País, Nasar y Gruber en el New Yorker, bloggers varios), y ahora un amigo me avisa que Yau los acusa de difamación. A Nassar, Gruber y el New Yorker, por ahora, pero también hay bloggers que han recibido el link en forma anónima sin otros comentarios (ars mathematica), y efectivamente en el anteúltimo parrafo del escrito que sus abogados enviaron a Nassar y Cía piden que se retracten el diario y menciona los blogs.
Recuerdo que cuando leí el artículo de Nasar y Gruber (me lo envió este mismo amigo) me pareció tan malo que decidí no linkearlo; también intenté una defensa de Yau en un blog español que lo atacó duramente (pero se hicieron los pelotudos y ni me contestaron, espero que no les llegue ahora una demanda a ellos también :P).
Linda novelita se vino... y eso que todavía el Clay no se pronunció sobre el millón de dólares, ni nadie lo reclamó.
Más posts al respecto: acá, cuando se confirmó que Perelman ganaba la Field; motl; woit; kottke; asymptotia; y también blogs no matemáticos como regret the error o infropoc.
19.9.06
1182.- Comentando noticias estilo webs dos punto cero
(Clarín) La actitud de T provocó la inmediata respuesta de indignación del resto de los plateístas que vieron la acción. Se vio a uno de ellos lanzarse sobre T y golpearlo hasta entregarlo a la Policía. [el otro hincha había tirado un encendedor al juez de línea]
\
Tags: collaborative networks; community; community feedback; emergent behaviour; karma; order emergence; moderation system; peer pressure; peer to peer interaction; reputation system; synergy
\
Tags: collaborative networks; community; community feedback; emergent behaviour; karma; order emergence; moderation system; peer pressure; peer to peer interaction; reputation system; synergy
16.9.06
14.9.06
1180.- Ahora entiendo un poco mas...
...no sobre las elecciones Mexicanas, sino sobre el regreso de la democracia a Irak!
Vía este artículo que aparece hoy en el arxiv, me entero que el instituto que se encargó de las elecciones mexicanas fiscalizó las elecciones iraquíes y haitianas... (destaquemos que ambos lugares tienen tropas extranjeras que 'mantienen el orden').
Volviendo al paper, el argumento central es que la diferencia de votos entre los dos partidos cae dentro del margen de error del sistema que calculan, lo cual invalida la conclusión de quién ganó.
Dos notas extras:
1) El gráfico 1 es 'misleading', no conviene incluír curvas perturbadas sumándole un 13% (como en ese caso) porque se disimulan las fluctuaciones relativas (hubo gráficos mucho peores en este tema, donde se sumaron los partidos más chicos)
2) Las oscilaciones en los gráficos 8 en adelante se podrían atribuir al hierarchical growth...
3) No, eran sólo dos notas.
Vía este artículo que aparece hoy en el arxiv, me entero que el instituto que se encargó de las elecciones mexicanas fiscalizó las elecciones iraquíes y haitianas... (destaquemos que ambos lugares tienen tropas extranjeras que 'mantienen el orden').
Volviendo al paper, el argumento central es que la diferencia de votos entre los dos partidos cae dentro del margen de error del sistema que calculan, lo cual invalida la conclusión de quién ganó.
Dos notas extras:
1) El gráfico 1 es 'misleading', no conviene incluír curvas perturbadas sumándole un 13% (como en ese caso) porque se disimulan las fluctuaciones relativas (hubo gráficos mucho peores en este tema, donde se sumaron los partidos más chicos)
2) Las oscilaciones en los gráficos 8 en adelante se podrían atribuir al hierarchical growth...
3) No, eran sólo dos notas.
13.9.06
1179.- Traeme un fosforo
Sobre los estudiantes: "Un estudiante no es una bolsa a ser llenada sino una antorcha para ser encendida"
(Arnold, aquí)
(Arnold, aquí)
7.9.06
1178.- The Anscombe quartet...
...parece el título de una novela de Agatha Christie. Podemos adivinar los personajes: cuatro individuos mal entrazados, de origen tan oscuro que parecen inventados sólo para armar la historia, imposible imaginarlos juntos, pero que ahí están.
Y Poirot -no, mejor la vieja miss Marple, que contrasta más con los personajes- trata de identificar entre ellos al responsable de un crimen. Pero todos tienen sus motivos, sus historias, sus razones, sus coartadas -y todas se desarman convenientemente: podría decirse que ninguno tiene coartada-. Tan diferentes pero tan iguales a la vez, cuesta distinguir entre ellos al asesino. Ni siquiera se sabe si son cómplices o rivales.
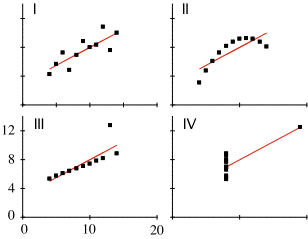
Los gráficos de arriba (tomados de aquí, que a su vez lo sacó de acá) corresponden a cuatro conjuntos de datos, conocidos como el Anscombe's quartet. Coinciden distintos parámetros estadísticos, se "ve" numéricamente que tienen la misma recta de cuadrados mínimos, aunque también se ve claramente en los gráficos que los datos son muy distintos.
No conocía el problema, me lo envía Osvaldo Gonzalez, y es algo así como la pesadilla de su área (data mining, inteligencia artificial). No alcanza con un programa que haga las cuentas y calcule promedios, varianzas, regresiones, errores... para distinguir entre distintos conjuntos de datos. Hace falta mirarlos, o programar algo que mire por uno.
Sospecho que merece mayor difusión (todavía no tiene página en la wikipedia, google da apenas 600 resultados), no sólo por el problema concreto del área, sino como advertencia para ciertos reduccionistas (las famosas power law de las que ya hemos hablado, este artículo que me pasara Weo hace tiempo, etc.).
Y Poirot -no, mejor la vieja miss Marple, que contrasta más con los personajes- trata de identificar entre ellos al responsable de un crimen. Pero todos tienen sus motivos, sus historias, sus razones, sus coartadas -y todas se desarman convenientemente: podría decirse que ninguno tiene coartada-. Tan diferentes pero tan iguales a la vez, cuesta distinguir entre ellos al asesino. Ni siquiera se sabe si son cómplices o rivales.

Los gráficos de arriba (tomados de aquí, que a su vez lo sacó de acá) corresponden a cuatro conjuntos de datos, conocidos como el Anscombe's quartet. Coinciden distintos parámetros estadísticos, se "ve" numéricamente que tienen la misma recta de cuadrados mínimos, aunque también se ve claramente en los gráficos que los datos son muy distintos.
No conocía el problema, me lo envía Osvaldo Gonzalez, y es algo así como la pesadilla de su área (data mining, inteligencia artificial). No alcanza con un programa que haga las cuentas y calcule promedios, varianzas, regresiones, errores... para distinguir entre distintos conjuntos de datos. Hace falta mirarlos, o programar algo que mire por uno.
Sospecho que merece mayor difusión (todavía no tiene página en la wikipedia, google da apenas 600 resultados), no sólo por el problema concreto del área, sino como advertencia para ciertos reduccionistas (las famosas power law de las que ya hemos hablado, este artículo que me pasara Weo hace tiempo, etc.).
1177.- Adicto
Y yo me creía adicto al mate...
Cuando leí que Manuel no conseguía yerba allá por Francia y titulaba su post "sindrome de abstinencia" no me imaginé que llegaría a pagar tres euros por cien gramos (si, más de 100 el kilo).
Mis más sinceras condolencias.
Cuando leí que Manuel no conseguía yerba allá por Francia y titulaba su post "sindrome de abstinencia" no me imaginé que llegaría a pagar tres euros por cien gramos (si, más de 100 el kilo).
Mis más sinceras condolencias.
5.9.06
1176.- Ig Nobel
Los Ig Nobel se entregan una vez al año a científicos y papers que bordean el ridículo, pero que no sólo nos hacen reir, sino también pensar (?). Para más info, ver aquí.
La gente que entrega los Ig Nobel edita un journal, Annals of Improbable Research, y también un blog (je, claro!), y por supuesto, un newsletter... y resulta que alguien respondió al newsletter y la respuesta nos llegó a todos los suscriptos. Enseguida empezaron varios a querer borrarse y el sistema no funciona. Los cruces ahora van y vienen como en cualquier lista de correos, aunque todos hablando de variantes lo mismo: robo de direcciones de mail, spam, etc.
El responsable, sin dudas, se ganó un Ig Nobel.
La gente que entrega los Ig Nobel edita un journal, Annals of Improbable Research, y también un blog (je, claro!), y por supuesto, un newsletter... y resulta que alguien respondió al newsletter y la respuesta nos llegó a todos los suscriptos. Enseguida empezaron varios a querer borrarse y el sistema no funciona. Los cruces ahora van y vienen como en cualquier lista de correos, aunque todos hablando de variantes lo mismo: robo de direcciones de mail, spam, etc.
El responsable, sin dudas, se ganó un Ig Nobel.
2.9.06
1175.- Y vos para quien trabajas?
Toda la matemática se divide en tres partes: criptografía (pagada por la CIA, KGB y similares), hidrodinámica (apoyada por los fabricantes de submarinos atómicos) y mecánica celeste (financiada por instituciones militares y otras que se ocupan de misiles, como la NASA).
V. Arnold, Mathematics: Frontiers and Perspectives, AMS 2000
La cita continúa, pero no tengo ganas de traducir:
Cryptography has generated number theory, algebraic geometry over finite felds, algebra (the creator of modern algebra, Viete, was the cryptographer of King Henry IV of France), combinatorics and computers.
Hydrodynamics procreated complex analysis, partial derivative equations, Lie groups and algebra theory, cohomology theory and scientific computing.
Celestial mechanics is the origin of dynamical systems, linear algebra, topology, variational calculus and symplectic geometry.
The existence of mysterious relations between all these different domains is the most striking and delightful feature of mathematics (having no rational explanation).
1.9.06
1174.- Ajedrez
Lo tengo un poco abandonado al tema, y me entero por Sertal que Kasparov volvió a las andadas, en un minimach todos contra todos -partida y revancha- con Karpov, Korchnoi y Polgar. Las tres K y la mejor mujer ajedrecista de la historia, nada menos.
De todos estos personajes, tal vez Korchnoi sea el menos conocido. A muchos les suena la rivalidad Kasparov-Karpov, pero antes hubo otras "dos K". Korchnoi enfrentó tres veces a Karpov por el título mundial (1975, 1978 y 1981) -aunque la primera era la final para ver quién enfrentaba a Fischer, que como no se presentó perdió el título frente a Karpov-. Luego, para el título del '84 quedaría en el camino cuando Kasparov le ganó, y ahí se abrió una nueva página de la historia. Korchnoi fue también el primer GM ruso en escaparse de la URSS en la década del setenta. Relegado durante mucho tiempo, no tenía oportunidades de competir en torneos internacionales, algo similar a lo que le ocurriría luego a Kasparov, aunque a éste lo salvó la Perestroika.
Lo más sorprendente es que para jugar este minitorneo pidió dos días libres de un torneo que jugaba en Bañolas, y pese al ida y vuelta... ganó ese torneo! Más aún, cuando volvió le ganó a Tiviakov (33 años, 2668 de elo -igual que Karpov-, puesto 39 del ranking mundial), que terminó segundo.
Korchoi es uno de los ajedrecistas injustamente despreciados -y hasta catalogado de loser- por no haber sido campeón mundial. Recuerdo que hará unos diez años "me acompañó" durante varios meses, cuando todas las noches reproducía una o dos partidas de su libro "400 best games" ...de 1978. En casi todos los partidos había un momento dondeparecía estar estaba perdido, pero se las ingeniaba para dar vuelta la situación. Ese afán por sobrevivir, esa capacidad por superar situaciones adversas, su espíritu de lucha son únicos.
Tiene apenas 75 años, y sigue dando batalla.
De todos estos personajes, tal vez Korchnoi sea el menos conocido. A muchos les suena la rivalidad Kasparov-Karpov, pero antes hubo otras "dos K". Korchnoi enfrentó tres veces a Karpov por el título mundial (1975, 1978 y 1981) -aunque la primera era la final para ver quién enfrentaba a Fischer, que como no se presentó perdió el título frente a Karpov-. Luego, para el título del '84 quedaría en el camino cuando Kasparov le ganó, y ahí se abrió una nueva página de la historia. Korchnoi fue también el primer GM ruso en escaparse de la URSS en la década del setenta. Relegado durante mucho tiempo, no tenía oportunidades de competir en torneos internacionales, algo similar a lo que le ocurriría luego a Kasparov, aunque a éste lo salvó la Perestroika.
Lo más sorprendente es que para jugar este minitorneo pidió dos días libres de un torneo que jugaba en Bañolas, y pese al ida y vuelta... ganó ese torneo! Más aún, cuando volvió le ganó a Tiviakov (33 años, 2668 de elo -igual que Karpov-, puesto 39 del ranking mundial), que terminó segundo.
Korchoi es uno de los ajedrecistas injustamente despreciados -y hasta catalogado de loser- por no haber sido campeón mundial. Recuerdo que hará unos diez años "me acompañó" durante varios meses, cuando todas las noches reproducía una o dos partidas de su libro "400 best games" ...de 1978. En casi todos los partidos había un momento donde
Tiene apenas 75 años, y sigue dando batalla.
30.8.06
1173.- Solution of the partuza problem
Ponele que te estás chamuyando a la hija de Yak Raian (o de Yak Bauer) en un sofá de dos cuerpos convenientemente girado hacia una pared por si los dos cuerpos se llegan a transformar en uno solo, mientras alrededor unas veinte personas andan en lo mismo en distintos rincones de la habitación, o bailan mientras suena una música que nadie llega a escuchar porque el volumen está muy alto, o hablan incoherencias entre sí en pequeños grupos. Convenientemente, dos terroristas islámicos (se los reconoce porque están de turbante y vestidos como beduinos aunque dentro de la habitación hacen como treinta grados, y sobre todo porque no beben bebidas alcohólicas y fuman de un narghile en lugar de prenderse a uno de los armados que circulan), decía que convenientemente estos dos planean vaya uno a saber qué cosa, amparados en el semianonimato de las tantas conversaciones simultáneas y sobre todo porque en lugares así nadie escucha a nadie, y sería fácil detectar si alguien está interesado en lo que dicen.
Pero Yak Raian (o Yak Bauer) está estacionado afuera en una combi anaranjada de esas para escolares con un equipo de altísima tecnología y un micrófono que capta todo lo que ahí dentro se dice.
Ahora, gracias a Casazza y Edidin (matemáticos de la universidad de Missouri), y a Balan de Siemens, se pueden reconstruír las distintas voces en forma independiente (la inversa de mezclar un disco a partir de varios canales de grabación: aquí, a partir de un único canal que graba todo, luego se separan las voces). Por supuesto, no hace falta adivinar quién financia estas cosas, lo pueden ver en la página de la universidad.
Y la pregunta, claro, es quién tiene que salir corriendo primero de la fiesta.
Pero Yak Raian (o Yak Bauer) está estacionado afuera en una combi anaranjada de esas para escolares con un equipo de altísima tecnología y un micrófono que capta todo lo que ahí dentro se dice.
Ahora, gracias a Casazza y Edidin (matemáticos de la universidad de Missouri), y a Balan de Siemens, se pueden reconstruír las distintas voces en forma independiente (la inversa de mezclar un disco a partir de varios canales de grabación: aquí, a partir de un único canal que graba todo, luego se separan las voces). Por supuesto, no hace falta adivinar quién financia estas cosas, lo pueden ver en la página de la universidad.
Y la pregunta, claro, es quién tiene que salir corriendo primero de la fiesta.
27.8.06
1172.- Las medallas Fields (2)
Los otros tres ganadores fueron Okounkou, Tao, y Werner.
Una primera observación, rápida y sin saber matemáticas (aunque conociendo el ambiente), es que los tres mandan todas sus cosas al arXiv. Y Perelman mandó ahí sus tres laburos. Ok, es razonable: son todos menores de 40 años, eso puede ser un signo de que son parte de una generación nueva.
Pero lo que más me asombró cuando leí las presentaciones de por qué recibía cada uno la medalla, fue la presencia en todos los casos de coautores: basta con mirar los pdfs de Okounkov, Tao y Werner para ver que sus trabajos fueron escritos muchas veces en coautoría con otras personas, a diferencia de los años anteriores (por ejemplo, comparar con el 2002 y el 1998). En el caso de Werner, él mismo dijo que sentía que el premio era compartido con Lawler y Schramm. Sobre Tao, están Green (que bien puede ganarla dentro de cuatro años si le da la edad, vean ésto), otros medallas Fields anteriores, y el famoso I-Team (sus coautores en muchos trabajos de la ecuación de Schroedinger, éste post muy irónico en geomblog parece demasiado duro al respecto). Por último, el post de Lubos Motl sobre Okounkov describe su interacción con físicos (publicó con C. Vafa, por ejemplo). Y de Perelman ya hablamos en el post 1170; pese a que sus tres trabajos los escribió solo, fueron más de diez matemáticos los que redondearon sus ideas (o las pasaron en limpio, si se quiere).
¿Es malo esto? ¿Son 'menos' ganadores de la Field? No lo creo, todo lo contrario. Me parece que el problema está en el modelo de la Field, de premiar individuos en una profesión cada vez más colectiva, y estos elegidos bien pueden ser el primer paso para hacer cambios. Para hacernos una idea de quiénes son realmente estos tipos, mencionemos que Tao lleva un promedio de un paper por mes en los últimos diez años (¡!). Okounkov entró en una línea de colaboración con los físicos que sigue los pasos de otro medalla Fields: Witten (y Witten es hoy día el más citado en física); no es fácil trabajar a tan gran nivel y ser reconocido tanto por los físicos y por los matemáticos. Werner, por otra parte, es el primero en ser premiado que trabaja en el área de probabilidades / procesos estocásticos. Y de Perelman, ni hablar: recordemos que el problema que resolvió estaba considerado uno de los siete más difíciles por cuya solución el Clay ofrece un millón de dólares.
Una primera observación, rápida y sin saber matemáticas (aunque conociendo el ambiente), es que los tres mandan todas sus cosas al arXiv. Y Perelman mandó ahí sus tres laburos. Ok, es razonable: son todos menores de 40 años, eso puede ser un signo de que son parte de una generación nueva.
Pero lo que más me asombró cuando leí las presentaciones de por qué recibía cada uno la medalla, fue la presencia en todos los casos de coautores: basta con mirar los pdfs de Okounkov, Tao y Werner para ver que sus trabajos fueron escritos muchas veces en coautoría con otras personas, a diferencia de los años anteriores (por ejemplo, comparar con el 2002 y el 1998). En el caso de Werner, él mismo dijo que sentía que el premio era compartido con Lawler y Schramm. Sobre Tao, están Green (que bien puede ganarla dentro de cuatro años si le da la edad, vean ésto), otros medallas Fields anteriores, y el famoso I-Team (sus coautores en muchos trabajos de la ecuación de Schroedinger, éste post muy irónico en geomblog parece demasiado duro al respecto). Por último, el post de Lubos Motl sobre Okounkov describe su interacción con físicos (publicó con C. Vafa, por ejemplo). Y de Perelman ya hablamos en el post 1170; pese a que sus tres trabajos los escribió solo, fueron más de diez matemáticos los que redondearon sus ideas (o las pasaron en limpio, si se quiere).
¿Es malo esto? ¿Son 'menos' ganadores de la Field? No lo creo, todo lo contrario. Me parece que el problema está en el modelo de la Field, de premiar individuos en una profesión cada vez más colectiva, y estos elegidos bien pueden ser el primer paso para hacer cambios. Para hacernos una idea de quiénes son realmente estos tipos, mencionemos que Tao lleva un promedio de un paper por mes en los últimos diez años (¡!). Okounkov entró en una línea de colaboración con los físicos que sigue los pasos de otro medalla Fields: Witten (y Witten es hoy día el más citado en física); no es fácil trabajar a tan gran nivel y ser reconocido tanto por los físicos y por los matemáticos. Werner, por otra parte, es el primero en ser premiado que trabaja en el área de probabilidades / procesos estocásticos. Y de Perelman, ni hablar: recordemos que el problema que resolvió estaba considerado uno de los siete más difíciles por cuya solución el Clay ofrece un millón de dólares.
26.8.06
1171.- Estadisticas auxiliares
Los siguientes números corresponden al promedio de autores por artículos de distintos journals para los años 1930, 1965 y 2005: los tradicionales Acta MAthematica, Annals de Princeton, Mathematische Annalen y Math Z alemanes, y las más 'nuevas' Arkiv for Math, Pacific J Math y Duke Math J.
1930: 1.035
1965: 1.219
2005: 1.706
Está claro que la cosa va en aumento, y hay detalles más finos para mirar.
Contra todo pronóstico, los papers del Acta y el Annals tienen significativamente más coautores en promedio: en 1930 (1.067), en 1965 (1.55), y en 2005 (1.85).
Parece que en 1930 la colaboración era escasa y entre grandes (tipo Hardy & Littlewood); en 1965 aparece un componente vertical (alumnos con sus directores, y se cruzan generaciones); mientras que en 2005 ya toma el aspecto de una orgía 'transgrediendo los bordes' de la raza humana. Y no es joda: en el 2005 el Annals publicó la demostración computarizada de Hales (que mencionamos acá), aunque éste no incluyó a la pobre máquina como coautora... (si creen que algo así sería inaceptable, es porque no oyeron hablar de Shalosh B. Ekhad).
1930: 1.035
1965: 1.219
2005: 1.706
Está claro que la cosa va en aumento, y hay detalles más finos para mirar.
Contra todo pronóstico, los papers del Acta y el Annals tienen significativamente más coautores en promedio: en 1930 (1.067), en 1965 (1.55), y en 2005 (1.85).
Parece que en 1930 la colaboración era escasa y entre grandes (tipo Hardy & Littlewood); en 1965 aparece un componente vertical (alumnos con sus directores, y se cruzan generaciones); mientras que en 2005 ya toma el aspecto de una orgía 'transgrediendo los bordes' de la raza humana. Y no es joda: en el 2005 el Annals publicó la demostración computarizada de Hales (que mencionamos acá), aunque éste no incluyó a la pobre máquina como coautora... (si creen que algo así sería inaceptable, es porque no oyeron hablar de Shalosh B. Ekhad).
24.8.06
1170.- Las medallas Fields (1)
Hace seis meses posteaba mis 'candidatos' a ganarla. Tao me parecía indiscutido, Perelman era un problema, los otros no estaban claros (revisando la lista de premios Clay, EMIS, postdocs de Princeton y otros, fui sacando los otros candidatos; los otros dos ganadores también figuraban en estas listas: Andrei Okounkov y Wendelin Werner).
Pero la estrella indiscutida fue Grigori Yakovlevich Perelman (hijo de Yakov Perelman, el de los libros de física y matemática recreativa, según la wikipedia -y una nota al margen: la wikipedia es la referencia oficial de la Unión Internacional de Matemáticos a las biografías de Perelman!). Es la estrella digo porque rechazó el premio, y porque según parece, hace unos tres años fue separado del instituto donde trabajaba, ahora se apartó de las matemáticas y vive con su madre en San Petersburgo.
[Esta historia merecería más cuidado al ser contada, por la cantidad de gente involucrada y porque todavía no está del todo clara.]
A grandes rasgos, en 2003 dio una serie de charlas en USA contando sus ideas sobre la conjetura de Poincare, y el consenso fue que con eso podía completarse la demostración. Sin embargo, más de uno le saltó al cuello: sus trabajos eran apenas 68 páginas repartidas en tres trabajos -¡muy cortos! cómo pueden ser tan revolucionarios- que mandó al arxiv -que no fueron enviados a ninguna revista especializada para que los publicaran!!-, y no pasaron el peer-review -aghh!-. Los aficionados al escepticismo verán que cumplía más de una de las reglas para ser considerado un chanta, y parece que esa fue la razón para que el instituto donde trabajaba no le renovara su contrato.
Pero entre los que habían ido a las charlas había buenos matemáticos, expertos en el tema, que se convencieron de que esas ideas eran correctas. Distintos grupos se pusieron a trabajar en una demostración completa y detallada, y así aparecieron hace muy poco tres demostraciones: la de Kleiner y Lott (Notes on Perelman's papers), la de Cao y Zhu (que posteé hace dos meses, demostración que causó mucho revuelo porque más de un escéptico se convencía ahora de que Perelman tenía razón y los trataba de ladrones a los chinos (?!)), y por último la de Morgan y Tian de hace unas semanas que apareció en el arxiv y será publicada por la AMS y el Clay -Morgan es uno de los expertos en el tema y habló en el ICM sobre esta conjetura-. En total, más de 1000 páginas que ahora sí se puede decir que son una demostración completa. Desde ya, todos dejan claro desde el mismo abstract que el crédito es de Perelman, y que se limitan a completar las cuentas...
Y queda, todavía, el tema del millón de dólares del Clay, ya que la conjetura de Poincaré era uno de los problemas...
Update 1170.1: no es el hijo del famoso Yakov, porque éste murió en el sitio de Leningrado en 1942 y Grigori nació en 1966... sin embargo, su padre se llamaba Yakov, sin dudas!
Update 1170.2: para Perelman y sus charlas del 2003, ver este post, y para una idea sobre la conjetura, este otro.
Pero la estrella indiscutida fue Grigori Yakovlevich Perelman (
[Esta historia merecería más cuidado al ser contada, por la cantidad de gente involucrada y porque todavía no está del todo clara.]
A grandes rasgos, en 2003 dio una serie de charlas en USA contando sus ideas sobre la conjetura de Poincare, y el consenso fue que con eso podía completarse la demostración. Sin embargo, más de uno le saltó al cuello: sus trabajos eran apenas 68 páginas repartidas en tres trabajos -¡muy cortos! cómo pueden ser tan revolucionarios- que mandó al arxiv -que no fueron enviados a ninguna revista especializada para que los publicaran!!-, y no pasaron el peer-review -aghh!-. Los aficionados al escepticismo verán que cumplía más de una de las reglas para ser considerado un chanta, y parece que esa fue la razón para que el instituto donde trabajaba no le renovara su contrato.
Pero entre los que habían ido a las charlas había buenos matemáticos, expertos en el tema, que se convencieron de que esas ideas eran correctas. Distintos grupos se pusieron a trabajar en una demostración completa y detallada, y así aparecieron hace muy poco tres demostraciones: la de Kleiner y Lott (Notes on Perelman's papers), la de Cao y Zhu (que posteé hace dos meses, demostración que causó mucho revuelo porque más de un escéptico se convencía ahora de que Perelman tenía razón y los trataba de ladrones a los chinos (?!)), y por último la de Morgan y Tian de hace unas semanas que apareció en el arxiv y será publicada por la AMS y el Clay -Morgan es uno de los expertos en el tema y habló en el ICM sobre esta conjetura-. En total, más de 1000 páginas que ahora sí se puede decir que son una demostración completa. Desde ya, todos dejan claro desde el mismo abstract que el crédito es de Perelman, y que se limitan a completar las cuentas...
Y queda, todavía, el tema del millón de dólares del Clay, ya que la conjetura de Poincaré era uno de los problemas...
Update 1170.1: no es el hijo del famoso Yakov, porque éste murió en el sitio de Leningrado en 1942 y Grigori nació en 1966... sin embargo, su padre se llamaba Yakov, sin dudas!
Update 1170.2: para Perelman y sus charlas del 2003, ver este post, y para una idea sobre la conjetura, este otro.
21.8.06
18.8.06
1168.- Problem(it)a
Esta vez, es un problema que me envía Guillermo Martínez (sí, éste), y que no tengo idea de cómo resolver:
Las preguntas que se derivan de esto son varias:
(creo que si..., pero no encontré referencias)
2) La fórmula general para responder las dos preguntas:
a) Si lanzo una moneda n veces, cuál es la cantidad de configuraciones distintas con rachas de longitud mayor o igual que k?
b) Si lanzo una moneda n veces, cuál es la mayor longitud k tal que la probabilidad de obtener una racha de longitud mayor o igual que k supere a 1/2?
(está claro que rachas de longitud k=1 siempre habrá, digamos que su probabilidad es 1; que k=n, esto es que todas salgan cara o ceca, son sólo dos posibilidades en 2^n, muy pequeña; cuando k va creciendo desde 1 hasta n, esa probabilidad cae de 1 a 1/2^(n-1)... ¿cuándo pasa por 1/2?)
Menciona en el mail una historia divertida: "un maestro divide a su curso en dos grupos. A los del grupo A les pide que traigan de sus casas una hoja con los resultados de lanzar una moneda 100 veces. A los del grupo B les pide que en vez de hacer los lanzamientos imaginen y escriban cómo les parece que sería una secuencia así. Al día siguiente el maestro mezcla las hojas y puede ir diciendo con sólo mirar las secuencias a qué grupo pertenece cada una, si a la real o a la imaginada. Lo que ocurre, por supuesto, es que la idea intuitiva de azar está asociada a la alternancia más que a las rachas. Pero cuando n es suficientemente grande, aparecen rachas cada vez más largas. El maestro elige como reales a las secuencias que tengan al menos una racha de longitud 6."
El pedido de GM es si alguien aporta mas info sobre el problema. Se escuchan ideas, soluciones, soluciones parciales, reflexiones varias. Mis opiniones también van a los comentarios.
si lanzamos una moneda 5 veces seguidas la probabilidad de que aparezca una racha de longitud mayor o igual que tres (ya sean tres caras o tres cruces), es un medio (16 configuraciones con rachas sobre 32 posibles). Si lanzamos la moneda 6 veces la probabilidad es de 38/64.
Las preguntas que se derivan de esto son varias:
1) Si es un problema que, por ejemplo, tenga nombre propio. Si se sabe quién estudió por primera vez estas rachas "críticas".
(creo que si..., pero no encontré referencias)
2) La fórmula general para responder las dos preguntas:
a) Si lanzo una moneda n veces, cuál es la cantidad de configuraciones distintas con rachas de longitud mayor o igual que k?
b) Si lanzo una moneda n veces, cuál es la mayor longitud k tal que la probabilidad de obtener una racha de longitud mayor o igual que k supere a 1/2?
(está claro que rachas de longitud k=1 siempre habrá, digamos que su probabilidad es 1; que k=n, esto es que todas salgan cara o ceca, son sólo dos posibilidades en 2^n, muy pequeña; cuando k va creciendo desde 1 hasta n, esa probabilidad cae de 1 a 1/2^(n-1)... ¿cuándo pasa por 1/2?)
3) Si alguien intentó una reflexión filosófica sobre estos "sesgos" del azar.
Menciona en el mail una historia divertida: "un maestro divide a su curso en dos grupos. A los del grupo A les pide que traigan de sus casas una hoja con los resultados de lanzar una moneda 100 veces. A los del grupo B les pide que en vez de hacer los lanzamientos imaginen y escriban cómo les parece que sería una secuencia así. Al día siguiente el maestro mezcla las hojas y puede ir diciendo con sólo mirar las secuencias a qué grupo pertenece cada una, si a la real o a la imaginada. Lo que ocurre, por supuesto, es que la idea intuitiva de azar está asociada a la alternancia más que a las rachas. Pero cuando n es suficientemente grande, aparecen rachas cada vez más largas. El maestro elige como reales a las secuencias que tengan al menos una racha de longitud 6."
El pedido de GM es si alguien aporta mas info sobre el problema. Se escuchan ideas, soluciones, soluciones parciales, reflexiones varias. Mis opiniones también van a los comentarios.
16.8.06
1167.- Linking
-Twisted Physics y el observatorio de Buenos Aires (si alguien lo conoce a Moledo, pásenle el link [no, el de mi post no, el del post de ella {bue, el mío también, si quieren}])
-Expandiendo el binomio.
-Theory of fun. (¿A qué se dedicaun matemático uno cuando juega? [Uno bien podría decir que el matemático se ocupa del reconocimiento de patrones y estructuras -desde el ladri que modifica una demostración ajena para aplicarla al problema al que se dedica, hasta el super capo que unifica teorías diferentes porque detecta su similitud... {eh, bueno... hay un consejo de Feynman al respecto, y las dos cosas no son tan diferentes}]) (vía Leuschke)
-El hombre que le va a decir "no" a un millón de dólares (hay gente que denigra a los chinos que dieron una demostración hace poco, tratándolos de ladris [zifra de blogalia, el diario El País de España... si se hubiesen molestado en buscar el paper de los chinos, verían que elevan "Perelman Theory" a la categoría de palabra clave del trabajo...] la versión oficial -real- va a aparecer en el icm la semana próxima, aquí está el abstract; un segundo grupo presentó una demostración, también bastante larga, que van a publicar la AMS y el Clay)
-Expandiendo el binomio.
-Theory of fun. (¿A qué se dedica
-El hombre que le va a decir "no" a un millón de dólares (hay gente que denigra a los chinos que dieron una demostración hace poco, tratándolos de ladris [zifra de blogalia, el diario El País de España... si se hubiesen molestado en buscar el paper de los chinos, verían que elevan "Perelman Theory" a la categoría de palabra clave del trabajo...] la versión oficial -real- va a aparecer en el icm la semana próxima, aquí está el abstract; un segundo grupo presentó una demostración, también bastante larga, que van a publicar la AMS y el Clay)
12.8.06
1166.- Esperemos que sea el primero de los muchos dominos por caer
La frase es de Baez, en referencia a la renuncia masiva (9 de 10) del editorial board del journal Topology.
La carta que enviaron hace dos días, renunciando desde fin de año, es el final de una batalla que lleva más de diez años. Existen otras cartas (como ésta) que el journal ignoró, otros editorial boards han resignado antes (por ejemplo, éste), e incluso las universidades han entrado a luchar contra los precios de los journals (ejemplo).
Related info:
-Imagine una editorial, post mío para uberbin pero perdido en las garras de su wp, que apunta al problema de fondo con las editoriales científicas.
-Se pudrió todo, sobre el boicot de las universidades yanquis.
-Knuth vs. el Journal of Algorithms.
-artículo en las Notices AMS.
-El año pasado, un journal de Elsevier se volvía Open Access hasta definir su política editorial (ver [vía Language Log]. El experimento parece haber terminado...
La carta que enviaron hace dos días, renunciando desde fin de año, es el final de una batalla que lleva más de diez años. Existen otras cartas (como ésta) que el journal ignoró, otros editorial boards han resignado antes (por ejemplo, éste), e incluso las universidades han entrado a luchar contra los precios de los journals (ejemplo).
Related info:
-Imagine una editorial, post mío para uberbin pero perdido en las garras de su wp, que apunta al problema de fondo con las editoriales científicas.
-Se pudrió todo, sobre el boicot de las universidades yanquis.
-Knuth vs. el Journal of Algorithms.
-artículo en las Notices AMS.
-El año pasado, un journal de Elsevier se volvía Open Access hasta definir su política editorial (ver [vía Language Log]. El experimento parece haber terminado...
9.8.06
1165.- Telefono descompuesto
No hay caso, los teléfonos están funcionando cada vez peor.
Heisenberg: no se pudo determinar la última cifra del número que ha marcado, por favor, mueva el teléfono e inténtelo de nuevo.
Pitágoras: el número que ha marcado elevado al cuadrado es distinto de 2, por favor, calcule más cifras e inténtelo de nuevo.
Cantor: el número que ha marcado no figura en nuestro listado, por favor, lea la guía en diagonal e inténtelo de nuevo.
Godel: el número que ha marcado corresponde a un teléfono que no se puede demostrar que lo sea, por favor, mándele una carta.
Erdos: el número que ha marcado no corresponde a Erdos, por favor, cámbielo con un nuevo coautor e inténtelo de nuevo.
Mandelbrot: el número que ha marcado es un entero, por favor, consiga uno fraccionario e inténtelo de nuevo.
Ramanujan: el número que ha marcado no se descompone como suma de dos cubos, por favor, busque otro e inténtelo de nuevo.
Descartes: el número que ha marcado no existe, por favor, piénselo e intente de nuevo.
Hamming: el número que ha marcado es incorrecto, por favor, sume uno al tercer dígito, reste dos del último, cámbiele el signo e inténtelo de nuevo.
L'Hôpital: el número que ha marcado no ha podido ser determinado, por favor, derívelo e inténtelo de nuevo.
Napier: el número que ha marcado es incorrecto, por favor, tómele logaritmos e inténtelo de nuevo.
Padé: el número que ha marcado es una pésima aproximación, por favor, inténtelo de nuevo con más dígitos.
Zermelo: el número que ha marcado está equivocado, por favor, elija otro de otra guía e inténtelo de nuevo.
Lindemann: el número que ha marcado no es trascendente, por favor, inténtelo de nuevo.
Bourbaki: el número que ha marcado no es lo suficientemente general, por favor, reemplace los dígitos por letras e inténtelo de nuevo.
Y los que funcionaron, me respondió un contestador:
Pauli: en este momento todos nuestros orbitales están ocupados, por favor, gire el teléfono a medias e inténtelo de nuevo.
Chaitin: en este momento estoy con un amigo, si es urgente disque Omega.
(hay un viejo chiste que dice "el número que ha marcado es imaginario, por favor, rote el teléfono 90 grados e inténtelo de nuevo")
Heisenberg: no se pudo determinar la última cifra del número que ha marcado, por favor, mueva el teléfono e inténtelo de nuevo.
Pitágoras: el número que ha marcado elevado al cuadrado es distinto de 2, por favor, calcule más cifras e inténtelo de nuevo.
Cantor: el número que ha marcado no figura en nuestro listado, por favor, lea la guía en diagonal e inténtelo de nuevo.
Godel: el número que ha marcado corresponde a un teléfono que no se puede demostrar que lo sea, por favor, mándele una carta.
Erdos: el número que ha marcado no corresponde a Erdos, por favor, cámbielo con un nuevo coautor e inténtelo de nuevo.
Mandelbrot: el número que ha marcado es un entero, por favor, consiga uno fraccionario e inténtelo de nuevo.
Ramanujan: el número que ha marcado no se descompone como suma de dos cubos, por favor, busque otro e inténtelo de nuevo.
Descartes: el número que ha marcado no existe, por favor, piénselo e intente de nuevo.
Hamming: el número que ha marcado es incorrecto, por favor, sume uno al tercer dígito, reste dos del último, cámbiele el signo e inténtelo de nuevo.
L'Hôpital: el número que ha marcado no ha podido ser determinado, por favor, derívelo e inténtelo de nuevo.
Napier: el número que ha marcado es incorrecto, por favor, tómele logaritmos e inténtelo de nuevo.
Padé: el número que ha marcado es una pésima aproximación, por favor, inténtelo de nuevo con más dígitos.
Zermelo: el número que ha marcado está equivocado, por favor, elija otro de otra guía e inténtelo de nuevo.
Lindemann: el número que ha marcado no es trascendente, por favor, inténtelo de nuevo.
Bourbaki: el número que ha marcado no es lo suficientemente general, por favor, reemplace los dígitos por letras e inténtelo de nuevo.
Y los que funcionaron, me respondió un contestador:
Pauli: en este momento todos nuestros orbitales están ocupados, por favor, gire el teléfono a medias e inténtelo de nuevo.
Chaitin: en este momento estoy con un amigo, si es urgente disque Omega.
(hay un viejo chiste que dice "el número que ha marcado es imaginario, por favor, rote el teléfono 90 grados e inténtelo de nuevo")
7.8.06
1164.- Sheckleyed (II)
De a poco, se reemplazaron las elecciones por muestreos estadísticos. No hacía falta que toda la población votara, un simple (y bien hecho) muestreo de la población era más que suficiente.
Luego, se redujo el número de personas que votaban en ese muestreo: era suficiente con una sola bien elegida. Las elecciones (e incluso las presidencias) pasaban a recordarse por el Elector, la de Fulano, la de Mengano, etc. No importaba siquiera el presidente, se recordaba al Elector. Y por supuesto, se le achacaban a los electores las faltas o méritos del mandato. Quién era esa persona, el Elector, era un secreto hasta pasada la elección, aunque la noticia se filtraba. Pero entonces había medidas de seguridad para evitar problemas, etcétera.
También el proceso de elección era secreto, sólo había suposiciones al respecto, pero la votación había sido reemplazada por un cuestionario. Preguntas -secretas- que se le hacían al Elector decidían el resultado.
Todo muy científico, preciso, exacto.
(Ese es uno de los méritos de Sheckley: ciencia ficción donde las ciencias son las sociales, con todo un avance inimaginable aún hoy día.)
El cuento cubre los días previos a la elección desde la óptica de un ciudadano. Cuenta cómo vive, sus preocupaciones ante la posibilidad de ser él el Elector cuando se sabe que será alguien de su zona, su barrio, finalmente él.
Y termina cuando revela cómo fue la elección.
Para no espoilear, el final está en los comments, puede obviarlo y leer el original, muchísimo mejor, aunque no recuerdo cómo se llama el cuento ni en qué libro salió. Es uno de los mejores cuentos de Sheckley
Es uno de los pocos cuentos de Asimov que me dan vueltas en la cabeza, y la elección de México me lo recordó. Para más datos -de México- este artículo (vía Santiago).
Upgrade 1164.1: Me avisa Markelo, con mucha razón, que el cuento es de Asimov, y me pasa un link.
Algún día tendría que analizar por qué rechazo tanto al Asimov cuentista. Sus libros y artículos de divulgación me parecen buenísimos, pero rechazo sus ficciones. Desde que leí un cuento de Brown que sintetiza en una página el cuento de "La última pregunta", lo desprecié como un autor con mucho oficio y pocas ideas (en el mismo espacio, Brown -o Sheckley- desparraman más ideas sin tantas vueltas). Ahora, esto me va a dejar reflexionando sobre qué otros cuentos de Asimov atribuyo a otra gente...
Upgrade 1164.2: releyendo el cuento, encuentro este párrafo y entiendo mejor por qué lo relaciono con México:
Pero mira, a veces llevaba toda la noche contar..., sí, hacer el recuento de lo que opinaban unos y otros, a quién habían votado. Todo el mundo se impacientaba. Por ello se inventaron máquinas especiales, capaces de comparar los primeros votos con los de los mismos lugares en años anteriores. De esta manera, la máquina preveía cómo se presentaba la votación en su conjunto y quién sería elegido.
Luego, se redujo el número de personas que votaban en ese muestreo: era suficiente con una sola bien elegida. Las elecciones (e incluso las presidencias) pasaban a recordarse por el Elector, la de Fulano, la de Mengano, etc. No importaba siquiera el presidente, se recordaba al Elector. Y por supuesto, se le achacaban a los electores las faltas o méritos del mandato. Quién era esa persona, el Elector, era un secreto hasta pasada la elección, aunque la noticia se filtraba. Pero entonces había medidas de seguridad para evitar problemas, etcétera.
También el proceso de elección era secreto, sólo había suposiciones al respecto, pero la votación había sido reemplazada por un cuestionario. Preguntas -secretas- que se le hacían al Elector decidían el resultado.
Todo muy científico, preciso, exacto.
(Ese es uno de los méritos de Sheckley: ciencia ficción donde las ciencias son las sociales, con todo un avance inimaginable aún hoy día.)
El cuento cubre los días previos a la elección desde la óptica de un ciudadano. Cuenta cómo vive, sus preocupaciones ante la posibilidad de ser él el Elector cuando se sabe que será alguien de su zona, su barrio, finalmente él.
Y termina cuando revela cómo fue la elección.
Es uno de los pocos cuentos de Asimov que me dan vueltas en la cabeza, y la elección de México me lo recordó. Para más datos -de México- este artículo (vía Santiago).
Upgrade 1164.1: Me avisa Markelo, con mucha razón, que el cuento es de Asimov, y me pasa un link.
Algún día tendría que analizar por qué rechazo tanto al Asimov cuentista. Sus libros y artículos de divulgación me parecen buenísimos, pero rechazo sus ficciones. Desde que leí un cuento de Brown que sintetiza en una página el cuento de "La última pregunta", lo desprecié como un autor con mucho oficio y pocas ideas (en el mismo espacio, Brown -o Sheckley- desparraman más ideas sin tantas vueltas). Ahora, esto me va a dejar reflexionando sobre qué otros cuentos de Asimov atribuyo a otra gente...
Upgrade 1164.2: releyendo el cuento, encuentro este párrafo y entiendo mejor por qué lo relaciono con México:
Pero mira, a veces llevaba toda la noche contar..., sí, hacer el recuento de lo que opinaban unos y otros, a quién habían votado. Todo el mundo se impacientaba. Por ello se inventaron máquinas especiales, capaces de comparar los primeros votos con los de los mismos lugares en años anteriores. De esta manera, la máquina preveía cómo se presentaba la votación en su conjunto y quién sería elegido.
5.8.06
1163.- Sheckleyed
Stanislaw Lem, Fredric Brown y Robert Sheckely son mis escritores de ciencia ficción favoritos. El rasgo distintivo que los une es el humor, y cada uno lo manejaba a su manera.
Sheckley (que usted tal vez lo conozca por la película 'La décima víctima', verdadero asesinato de un cuento maravilloso) hace reír con situaciones absurdas, pero cada tanto aparecen situaciones reales que parecen salidas de sus cuentos.
La decisión en México de dar por terminada la elección sin un recuento total, a partir de un recuento de menos del diez por ciento, es una de ellas.
Sheckley (que usted tal vez lo conozca por la película 'La décima víctima', verdadero asesinato de un cuento maravilloso) hace reír con situaciones absurdas, pero cada tanto aparecen situaciones reales que parecen salidas de sus cuentos.
La decisión en México de dar por terminada la elección sin un recuento total, a partir de un recuento de menos del diez por ciento, es una de ellas.
27.7.06
1161.- 1416141614161416...
Directamente le afano el post a Hernán:
Irracionalidad periódica
Se trata de un plan para combatir la inseguridad, dice La Nación.
Y los que no podemos asociarlo con ningún número periódico, ¿podremos llamar igual?
Irracionalidad periódica
Se trata de un plan para combatir la inseguridad, dice La Nación.
...el número de emergencia *31416 - que ya está funcionando a modo de prueba y que el denunciante puede asociar con el número periódico Pi.
Y los que no podemos asociarlo con ningún número periódico, ¿podremos llamar igual?
26.7.06
1160.- Buscado

(No vamos a aclarar acá las preferencias de nadie al respecto, todo se origina en esta nota)
Suscribirse a:
Comentarios (Atom)

